Page 43 -
P. 43
โครงการหนังสืออิเล็กทรอนิกส์ เฉลิมพระเกียรติสมเด็จพระเทพรัตนราชสุดาฯ สยามบรมราชกุมารี
A 2 2
2
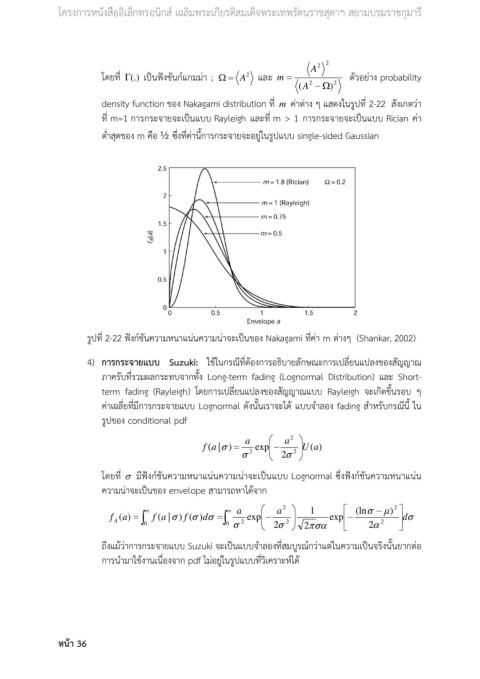
โดยที่ (.)Γ เปนฟงชันกแกมมา ; Ω = A และ m = ตัวอยาง probability
(A 2 − Ω ) 2
density function ของ Nakagami distribution ที่ m คาตาง ๆ แสดงในรูปที่ 2-22 สังเกตวา
ที่ m=1 การกระจายจะเปนแบบ Rayleigh และที่ m > 1 การกระจายจะเปนแบบ Rician คา
ต่ําสุดของ m คือ ½ ซึ่งที่คานี้การกระจายจะอยูในรูปแบบ single-sided Gaussian
รูปที่ 2-22 ฟงกชันความหนาแนนความนาจะเปนของ Nakagami ที่คา m ตางๆ (Shankar, 2002)
4) การกระจายแบบ Suzuki: ใชในกรณีที่ตองการอธิบายลักษณะการเปลี่ยนแปลงของสัญญาณ
ภาครับที่รวมผลกระทบจากทั้ง Long-term fading (Lognormal Distribution) และ Short-
term fading (Rayleigh) โดยการเปลี่ยนแปลงของสัญญาณแบบ Rayleigh จะเกิดขึ้นรอบ ๆ
คาเฉลี่ยที่มีการกระจายแบบ Lognormal ดังนั้นเราจะได แบบจําลอง fading สําหรับกรณีนี้ ใน
รูปของ conditional pdf
2
a a
f (a |σ ) = exp− U (a )
σ 2 2σ 2
โดยที่ σ มีฟงกชันความหนาแนนความนาจะเปนแบบ Lognormal ซึ่งฟงกชันความหนาแนน
ความนาจะเปนของ envelope สามารถหาไดจาก
a
f ( a = ∫ 0 ∞ f ( a | σ f () σ d ) σ = ∫ 0 ∞ σ 2 exp − 2 a 2 2 π 2 1 σα exp (ln σ − 2 µ) 2 d σ
−
)
A
σ
2
α
ถึงแมวาการกระจายแบบ Suzuki จะเปนแบบจําลองที่สมบูรณกวาแตในความเปนจริงนั้นยากตอ
การนํามาใชงานเนื่องจาก pdf ไมอยูในรูปแบบที่วิเคราะหได
หนา 36