Page 42 -

P. 42

∞
โครงการหนังสืออิเล็กทรอนิกส์ เฉลิมพระเกียรติสมเด็จพระเทพรัตนราชสุดาฯ สยามบรมราชกุมารี

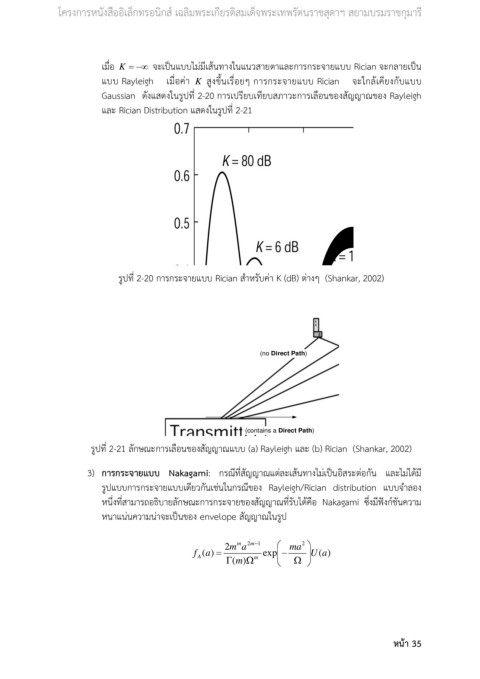
เมื่อ K = −∞ จะเปนแบบไมมีเสนทางในแนวสายตาและการกระจายแบบ Rician จะกลายเปน
แบบ Rayleigh เมื่อคา K สูงขึ้นเรื่อยๆ การกระจายแบบ Rician จะใกลเคียงกับแบบ

Gaussian ดังแสดงในรูปที่ 2-20 การเปรียบเทียบสภาวะการเลือนของสัญญาณของ Rayleigh
และ Rician Distribution แสดงในรูปที่ 2-21

รูปที่ 2-20 การกระจายแบบ Rician สําหรับคา K (dB) ตางๆ (Shankar, 2002)

(no Direct Path)

(contains a Direct Path)
รูปที่ 2-21 ลักษณะการเลือนของสัญญาณแบบ (a) Rayleigh และ (b) Rician (Shankar, 2002)

3) การกระจายแบบ Nakagami: กรณีที่สัญญาณแตละเสนทางไมเปนอิสระตอกัน และไมไดมี
รูปแบบการกระจายแบบเดียวกันเชนในกรณีของ Rayleigh/Rician distribution แบบจําลอง

หนึ่งที่สามารถอธิบายลักษณะการกระจายของสัญญาณที่รับไดคือ Nakagami ซึ่งมีฟงกชันความ
หนาแนนความนาจะเปนของ envelope สัญญาณในรูป

2
2m m a 2m− 1  ma 
f A (a ) = Γ (m )Ω m exp− Ω  U (a )





หนา 35

37 38 39 40 41 42 43 44 45 46 47