Page 70 -

60
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์

× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
60
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า

น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม์
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ
2
จากสูตรที่ 1 
a
1
n
2
i
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
1
4
2
3
i
(n−1)
m i N
4
2
2
2

2
1
2
จากสูตรที่ 1 
a

2
n
ൌ (
i
] − N ส่วนค่า m , m , m และ m
(1)= ∑ [
1
1
4
i
3
2
(n−1) = ∑ [ (70) +(60) +(60) +(50) 2 ) −240 มีค่าเท่ากับ
m i N
4
(240)
โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว
4
14,600
) −240 = 243.33 − 240 = 3.33
2
2
2
ൌ ((70) +(60) +(60) +(50) 2
 2 ൌ ( บทที่ 1 องค์ประกอบทางพันธุกรรมและการเข้าสู่สมดุลของประชากร 63
60
(1) 1 ) −240
และการเข้าสู่สมดุลของประชากร 63
(240)
4 บทที่ 1 องค์ประกอบทางพันธุกรรม
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
14,600
ൌ ( ) −240 = 243.33 − 240 = 3.33
2
ൌ 3.841
60
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
0.1222N

0.1222N
2
52 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
8
=
.
4

1

3
3N
คนละโครโมโซม
0.0407N 3N ൌ 3.841
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
52 เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้ 0.0407N = orthogonal

3.841

พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
จีโนไทป์
จ านวนต้น
3.841
Locus B
พ่อ คนละโครโมโซม N Locus A ൌ 0.0407 Linkage
3.841

. ในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
เมื่อมีการผสมพันธุ์กันอย่างสุ่ม . . N . = 1 orthogonal 1 1

AaBb
70
จีโนไทป์ จ านวนต้น ͻͶǤ͵ͳ
แม่ ൌ 0.0407

Aabb
1
-1
-1 ge
Locus A
พ่อ 0.1678AABB 0.0944AABb 60 0.0531AaBb Locus B Linka
.
0.0944AaBB

aaBb
AaBb
-1 1
. 0.0944AABb ͲǤͲͷ͵ͳAAbb 60 70 . = 9 4 . 3 1 1 1 -1 1
0.0299Aabb
0.0531AaBb
.
.
.
แม่ 0.0531AaBb เมื่อท าการค านวณค่าสังเกต a และ a
. 0.0944AaBB aabb 0.0531aaBB 0.0299aaBb
2
1
-1 1
Aabb
0.0531AaBb
0.0299aaBb
0.0168aabb
.
. 0.1678AABB 0.0944AABb 50 60 0.0531AaBb -1 -1 1 -1
0.0299Aabb
0.0944AaBB
ค�านวณค่าสังเกต a และ a 1.964×94.31
จ านวนค่าสังเกตของจีโนไทป์ A_ =
-1
aaBb
. 0.0944AABb ͲǤͲͷ͵ͳAAbb 60 1 2 0.0299Aabb = 62.49 1 -1
0.0531AaBb
(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
1.964 x 94.31
. 0.0944AaBB 0.0531AaBb 0.0531aaBB 0.0299aaBb 2.964
0.1678AABB 0.1887 AABb 0.0531AAbb 1
aabb
-1
จ�านวนค่าสังเกตของจีโนไทป์ A = = 62.49 -1
50
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
ความถี่ของจีโนไทป์ในรุ่นลูก
. 0.0531AaBb = 0.0299Aabb 0.0299aaBb 0.0597Aabb] 1 2.964
0.0168aabb
0.2123AaBb
94.3
[0.1887AaBB
จ านวนค่าสังเกตของจีโนไทป์ aa = = 31.82

0.0531aaBB
0.0168aabb
0.0597 aaBb
(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 94.31
1 2.964
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
จ�านวนค่าสังเกตของจีโนไทป์ aa = = 31.82
2.964
1 2 1 2
0.1678AABB 0.1887 AABb 0.0531AAbb
2
จากนั้นท าการทดสอบไคสแควร์ว่าจะต้องใช้จ านวนต้นเท่าไหร่ถึงจะยอมรับอัตราส่วนที่ต้องการ
ความถี่ของจีโนไทป์ในรุ่นลูก
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
การทดสอบประชากรที่อยู่ในสภาวะสมดุล = เท่ากับ 50+60 = 110 แทนค่าสูตร 0.0597Aabb]
0.2123AaBb
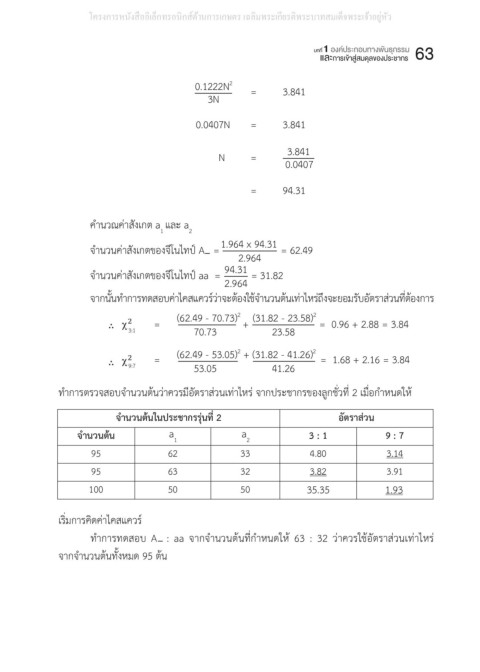
จากนั้นท�าการทดสอบค่าไคสแควร์ว่าจะต้องใช้จ�านวนต้นเท่าไหร่ถึงจะยอมรับอัตราส่วนที่ต้องการ
[0.1887AaBB

0.0531aaBB 0.0597 aaBb 0.0168aabb
1
(62.49 - 70.73) (31.82 - 23.58)
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 2= 130 และ a มีค่า
2 1
2
2
2
1
2
(31.8

2
22
]
(62.49 − 70.73)
+ = 0.96 + 2.88 = 3.84
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร  2 2 n ( − ) − 23.58) = 0.96+2.88 = 3.84
)

2
(O i −E i
∴  = ∑
ൌ
= [ +
การทดสอบประชากรที่อยู่ในสภาวะสมดุล เท่ากับ 50+60 = 110 แทนค่าสูตร E i 70.73 23.58 23.58
3:1

3:1
ൌ i=1
(1)
70.73

ก าหนดให้ 2 (62.49 − 53.05) (62.49 - 53.05) + (31.82 - 41.26) 2
2
1 2
1
= 1.68+2.16 =3.84
(31.82 −
2 41
2.26)

[ (130)− (110)]
2
2

]
)
ൌ
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร  = ∑ n ( 2 − ) = 1.68 + 2.16 = 3.84
2
+
(O i −E i
2
ൌ = [
9:7
9:7
∴  53.05

(1) ൌ i=1 1 1 53.05 41.26 41.26
E i
× ×240
 = ค่าไคสแควร์
2
2 2

ก าหนดให้ ท าการตรวจสอบจ านวนต้นว่าควรมีอัตราส่วนเท่าไหร่ จากประชากรของลูกชั่วที่ 2 เมื่อก าหนดให้
1
1
2
2
(20) (130)− (110)]
[
400
i = ค่าที่ได้จากการทดลองของลักษณะที่ i
O ท�าการตรวจสอบจ�านวนต้นว่าควรมีอัตราส่วนเท่าไหร่ จากประชากรของลูกชั่วที่ 2 เมื่อก�าหนดให้
2
2
=
ൌ

ൌ

1 1
240
240
× ×240
 E = ค่าไคสแควร์ จ านวนต้นในประชากรรุ่นที่ 2 อัตราส่วน
i = ค่าที่คาดหมายของลักษณะที่ i
2
2 2
(20)
n i = ค่าที่ได้จากการทดลองของลักษณะที่ i
O = จ านวนลักษณะที่ท าการทดสอบ จ านวนต้น ൌ a 2 = 400 2 3 : 1 9 : 7
a

240 1

240
i = ค่าที่คาดหมายของลักษณะที่ i
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส 33 4.80 3.14
E
95
62
n
= จ านวนลักษณะที่ท าการทดสอบ
95
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล 63 32 3.82 3.91
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส 50 35.35 1.93
33.33
1.59
50
100
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น

แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
เริ่มจากการคิดไคสแควร์
เริ่มการคิดค่าไคสแควร์
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่ ท�าการทดสอบ A : aa จากจ�านวนต้นที่ก�าหนดให้ 63 : 32 ว่าควรใช้อัตราส่วนเท่าไหร่
ท าการทดสอบ A_ : aa จากจ านวนต้นที่ก าหนดให้ 63 : 32 ว่าควรใช้อัตราอะไร จากจ านวนต้น
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
จากจ�านวนต้นทั้งหมด 95 ต้น
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
ทั้งหมด 95 ต้น
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่
1 110+ (70)
1
20+ (70)
∴ ความถี่ของยีน A = 2 = 0.275 และ ความถี่ของยีน a = 2 = 0.725

ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
200 200
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
1
1
110+ (70)
20+ (70)
∴ ความถี่ของยีน A = 2 = 0.275 และ ความถี่ของยีน a = 2 = 0.725
200 200
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200 = (0.275) × 200
2
2
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200 = (0.275) × 200
2
2