Page 170 -
P. 170
52
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
52
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
52
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
พ่อ
เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
พ่อ
.
.
.
.
.
แม่
.
.
แม่
พ่อ
0.0944AABb
0.0531AaBb
.
0.0944AaBB
0.1678AABB
.
.
0.1678AABB
.
0.0944AaBB
.
.
0.0531AaBb
0.0944AABb
0.0944AABb
0.0299Aabb
ͲǤͲͷ͵ͳAAbb
.
0.0531AaBb
แม่
0.0531AaBb
0.0299Aabb
0.0944AABb
ͲǤͲͷ͵ͳAAbb
.
0.0944AaBB
0.0531AaBb
.
0.0531aaBB
0.0299aaBb
0.0531AaBb
0.0531AaBb
0.0944AaBB
0.0299aaBb
0.1678AABB
.
0.0944AaBB
0.0944AABb
.
0.0531aaBB
.
0.0531AaBb
0.0299aaBb
0.0168aabb
0.0299Aabb
0.0944AABb
0.0299Aabb
0.0531AaBb
ͲǤͲͷ͵ͳAAbb
.
0.0168aabb
0.0531AaBb
0.0299aaBb
.
0.0299Aabb
0.0531AaBb
.
0.0531aaBB
0.0944AaBB
0.0299aaBb
0.1678AABB 0.1887 AABb 0.0531AAbb
0.0299aaBb
0.0299Aabb
0.0531AaBb
0.0168aabb
. เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้ .
=
0.0597Aabb]
โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว
0.2123AaBb
[0.1887AaBB
ความถี่ของจีโนไทป์ในรุ่นลูก 0.1678AABB 0.1887 AABb 0.0531AAbb
ความถี่ของจีโนไทป์ในรุ่นลูก = [0.1887AaBB 0.2123AaBb 0.0597Aabb]
0.0168aabb
0.0531aaBB
0.0597 aaBb
52 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 0.1678AABB 0.1887 AABb 0.0531AAbb
0.0597 aaBb
0.0168aabb
0.0531aaBB
ความถี่ของจีโนไทป์ในรุ่นลูก = [0.1887AaBB 0.2123AaBb 0.0597Aabb]
บทที่ 7 การศึกษาความแปรปรวน
163
52 การทดสอบประชากรที่อยู่ในสภาวะสมดุล บทที่ 7 กำรศึกษำควำมแปรปรวนของประชำกรโดยใช้เครื่องหมำยโมเลกุล 163
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
การทดสอบประชากรที่อยู่ในสภาวะสมดุล 0.0531aaBB 0.0597 aaBb 0.0168aabb ของประชากรโดยใช้เครื่องหมายโมเลกุล
เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
2 n (O i −E i ) 2 2
2 - E | - 0.5] ]
การทดสอบประชากรที่อยู่ในสภาวะสมดุล
[|O[
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร = ∑
2
]
)
พ่อ นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร 2 2 = ∑ n [|O −E |−0.5] E i E i
เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
จากสูตร
i
(O i −E i i=1
i
i
= [
จำกสูตร = i=1
E i
E
.
แม่ ก าหนดให้ . . 2 . i ) 2 ] i
n
52
(O i −E i
52 ดให้
พ่อ นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร = ∑ [ 2ค่าไคสแควร์ ค่ำไคสแควร์
ก าหน
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
= i=1
=
E i
. 0.1678AABB 0.0944AABb 0.0944AaBB 0.0531AaBb
.
.
.
.
2
=
แม่ 2 0.0944AABb = ค่าไคสแควร์ O = O ค่าสังเกต
ก าหนดให้
. = ค่าไคสแควร์ ͲǤͲͷ͵ͳAAbb 0.0531AaBb i 0.0299Aabb ค่ำสังเกต
i
ค่าคาดหวัง
E
=
i = ค่าที่ได้จากการทดลองของลักษณะที่ i
0.0299aaBb
0.0531AaBb
0.0944AaBB
0.0531aaBB
0.0944AABb
0.0531AaBb
. . เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้ O เมื่อมีการผสมพันธุ์กันอย่างสุ่มในประชากร จะมีความถี่ของจีโนไทป์ที่เกิดขึ้นดังนี้
0.0944AaBB
0.1678AABB
ค่ำคำดหวัง
=
E
i
i = ค่าที่ได้จากการทดลองของลักษณะที่ i
i
ͲǤͲͷ͵ͳAAbb
0.0944AABb
O 2 0.0531AaBb
.
0.0299aaBb
0.0168aabb
. = ค่าไคสแควร์ 0.0299Aabb 0.0531AaBb 0.0299Aabb
E
0.0944AaBB = ค่าที่คาดหมายของลักษณะที่ i
พ่อ พ่อ 0.0531AaBb
. E i 0.0531aaBB 0.0299aaBb
i = ค่าที่คาดหมายของลักษณะที่ i
. ที่ i
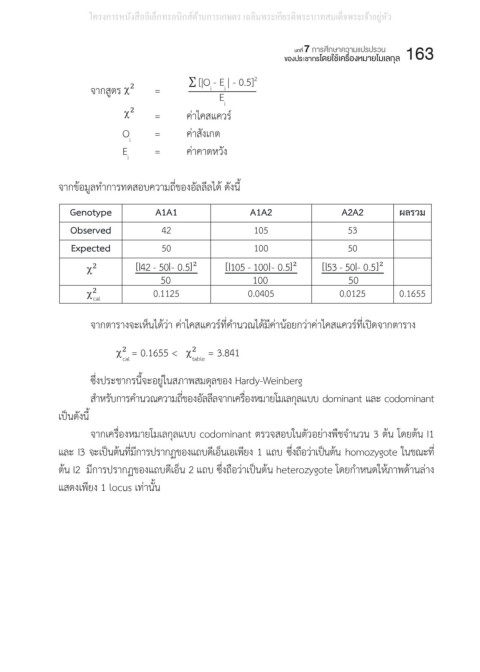
จากข้อมูลท�าการทดสอบความถี่ของอัลลีลได้ ดังนี้
n
จำกข้อมูลท ำกำรทดสอบควำมถี่ของอัลลีลได้ดังนี้
.
. .
. .
0.0168aabb
= จ านวนลักษณะที่ท าการทดสอบ
. 0.0299Aabb
i = ค่าที่ได้จากการทดลองของลักษณะ0.0299aaBb
. O 0.0531AaBb 0.1678AABB 0.1887 AABb 0.0531AAbb .
แม่ n แม่
ความถี่ของจีโนไ = จ านวนลักษณะที่ท าการทดสอบ 0.2123AaBb 0.0597Aabb]
E ทป์ในรุ่นลูก
=
i = ค่าที่คาดหมายของลักษณะที่ i
[0.1887AaBB
0.0531AaBb .0944AaBB ระชากรมีค่าไคส
0.167วร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าป
A1A2
A1A1
0.0944AABb 8AABB
0.0944AaBB 0.0944AABb
0.1678AABB .
0
. และเมื่อท าการค านวณไคสแค Genotype 0.0168aabb 0.0531AaBb A2A2 ผลรวม
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส
0.0531aaBB
0.0597 aaBb
0.1678AABB 0.1887 AABb 0.0531AAbb
. n
= จ านวนลักษณะที่ท าการทดสอบ
0.0531AaBb AAbb
0.0944AABb .
ͲǤͲͷ͵ͳ
0
0.0944AA
ͲǤͲͷ͵ͳAAbb Bb
0.0299Aabb .0531AaBb
ความถี่ของจีโนไทป์ในรุ่นลูก = [0.1887AaBB Observed 0.0597Aabb] 0.0299Aabb 53
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล
105
42
0.2123AaBb
0.0531AaBb AaBB
0.0944
0.0299aaBb .0531aaBB
0.0944AaBB .
0.0531aaBB 0.0531AaBb
.
การทดสอบประชากรที่อยู่ในสภาวะสมดุล 0.0531aaBB 0.0597 aaBb 0 0.0299aaBb
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล 0.0168aabb
Expected
100
50
0.053
0.0299Aabb 1AaBb
0.0168aabb .0299aaBb
0.0299aaBb 0.0299Aabb
0.0168aabb
0.0531AaBb .
0
. จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น 50
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
การทดสอบประชากรที่อยู่ในสภาวะสมดุล = ∑ n [|42−50|−0.5] 2 [|105−100|−0.5] 2 [|53−50|−0.5] 2
42 - 50 - 0.5
- 0.5
53 - 50
105 - 100 - 0.5
2
]
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร
)
(O i −E i
2
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
[
0.1678AABB
0.1887 AABb 0.0531AAbb0.1678AABB 0.1887 AABb 0.0531AAbb
i=1
50 50
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม 100 50 50
E i
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ปร
ความถี่ของจีโนไทป์ในรุ่นลูก ความถี่ของจีโนไทป์ในรุ่นลูก ะกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
0.0597Aabb]
=
0.0597Aabb]
[0.1887AaBB =
100
[
0.2123AaBb0.1887AaBB 2
ก าหนดให้ ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่ 0.0531aaBB 0.0597 aaBb0.0531aaBB ] 0.2123AaBb 0.0168aabb 0.0125 0.1655
0.0405
)
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร
n
(O i −E i
2
[
= ∑
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่
0.1125 0.0168aabb0.0597 aaBb
cal
i=1
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
E i
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
ก าหนดให้ ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่ จากตารางจะเห็นได้ว่า ค่าไคสแควร์ที่ค�านวณได้มีค่าน้อยกว่าค่าไคสแควร์ที่เปิดจากตาราง
= ค่าไคสแควร์
2
การทดสอบประชากรที่อยู่ในสภาวะสมดุล การทดสอบประชากรที่อยู่ในสภาวะสมดุล
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
จำกตำรำงจะเห็นได้ว่ำค่ำไคสแควร์ที่ค ำนวณได้มีค่ำน้อยกว่ำค่ำไคสแควร์ที่เปิดจำกตำรำง
O 1 1 = 3.841
i = ค่าที่ได้จากการทดลองของลักษณะที่ i
= ค่าไคสแควร์
2
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
20+ (70)
110+
2
∴ ความถี่ของยีน A =
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) จากสูตร = ∑ จากสูตร 2 (70) ] = 0.725 (O i −E i 2 2 ]
= 0.275 และ ความถี่ของยีน a =
1
1
)
= 0.1655 < )
n
n
−E i
2
2
(O i 2
2
table
cal
20+ (70)
110+
= 0.1655 < = ∑
= 3.841 [
นิยมใช้การทดสอบค่าด้วยวิธีไคสแควร์ (Chi-square) (70)
[
∴ ความถี่ของยีน A = 2 = 0.275 และ ความถี่ของยีน a = cal 2 i=1 = 0.725 i=1 E i
i = ค่าที่คาดหมายของลักษณะที่ i
E
table
200
i = ค่าที่ได้จากการทดลองของลักษณะที่ i
200
O
E i
ซึ่งประชำกรนี้ควำมถี่ของอัลลีลจะอยู่ในสมดุลของ Hardy-Weinberg
200
200
1
n
1
จากการค านวณจ านวนต้น
ก าหนดให้ = จ านวนลักษณะที่ท าการทดสอบ ที่มีจีโน ไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
ซึ่งประชากรนี้จะอยู่ในสภาพสมดุลของ Hardy-Weinberg
110+ (70)
20+ (70)
∴ ความถี่ของยีน A =
= 0.725
i = ค่าที่คาดหมายของลักษณะที่ i
= 0.275 และ ความถี่ของยีน a =
E
ก าหนดให้ 2
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
2
ส ำหรับกำรค ำนวณควำมถี่ของอัลลีลจำกเครื่องหมำยโมเลกุลแบบ dominant และ codominant
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส
200
200
ส�าหรับการค�านวณความถี่ของอัลลีลจากเครื่องหมายโมเลกุลแบบ dominant และ codominant
n
=
จ านวนลักษณะที่ท าการทดสอบ
= ค่าไคสแควร์ = ค่าไคสแควร์
= (0.275) × 200
2
2
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200
2
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮ
2าร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล 2 = (0.275) × 200
เป็นดังนี้
เป็นดังนี้ 200
2
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p ×
O วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส
และเมื่อท าการค านวณไคสแควร์แล้
i =
i = ค่าที่ได้จากการทดลองของลักษณะที่ i ค่าที่ได้จากการทดลองของลักษณะที่ i
O
จากเครื่องหมายโมเลกุลแบบ codominant ตรวจสอบในตัวอย่างพืชจ�านวน 3 ต้น โดยต้น I1
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล = (0.275) × 200
จำกเครื่องหมำยโมเลกุลแบบ codominant ตรวจสอบในตัวอย่ำงพืชจ ำนวน 3 ต้น โดยต้น I1 และ
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
2
2
i = ค่าที่คาดหมายของลักษณะที่ i ค่าที่คาดหมายของลักษณะที่ i
i =
E
E
และ I3 จะเป็นต้นที่มีการปรากฏของแถบดีเอ็นเอเพียง 1 แถบ ซึ่งถือว่าเป็นต้น homozygote ในขณะที่
I3 จะเป็นต้นที่มีกำรปรำกฏของแถบดีเอ็นเอเพียง 1 แถบ ซึ่งถือว่ำเป็นต้น homozygote ในขณะที่ต้น I2 มี
n
n และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
ดอกสีชมพู (Aa) 70 ต้น = จ านวนลักษณะที่ท าการทดสอบ จ านวนลักษณะที่ท าการทดสอบ
=
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
ต้น I2 มีการปรากฏของแถบดีเอ็น 2 แถบ ซึ่งถือว่าเป็นต้น heterozygote โดยก�าหนดให้ภาพด้านล่าง
กำรปรำกฏของแถบดีเอ็น 2 แถบ ซึ่งถือว่ำเป็นต้น heterozygote โดยก ำหนดให้ภำพที่แสดงเพียง 1 locus
และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส หรือไม่
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์ก และเมื่อท าการค านวณไคสแควร์แล้วเปรียบเทียบกับตารางไคสแควร์ พบว่า ถ้าประชากรมีค่าไคส
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
แสดงเพียง 1 locus เท่านั้น
แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล แควร์ที่น้อยกว่าค่าไคสแควร์ที่เปิดจากตารางแปลว่า ประชากรจะอยู่ในสมดุล
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่ เท่ำนั้น
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a 110+ (70)
1
จากตัวอย่างในประชากรที่มียีนควบคุม 1 ยีน ประกอบด้วยลักษณะที่ปรากฏดอกสีแดง (AA) 20 ต้น 1
20+ (70)
∴ ความถี่ของยีน A = 2 = 0.275 และ ความถี่ของยีน a = 2 = 0.725
ดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตามดอกสีชมพู (Aa) 70 ต้น และดอกสีขาว (aa) 110 ต้น ท าการตรวจสอบความถี่ของจีโนไทป์ว่าเป็นไปตาม
200 200
1 110+ (70)
1
20+ (70)
∴ ความถี่ของยีน A = 2 = 0.275 และ ความถี่ของยีน a = 2 = 0.725
ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่ ความถี่ของกฎฮาร์ดี-ไวน์เบิร์กหรือไม่
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
200 200
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
ก าหนดให้ p คือ ความถี่ของยีน A และ q คือความถี่ของยีน a
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200 = (0.275) × 200
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
2
2
1 1 1 1
20+ (70)
20+ (70)
110+ (70)
2
2
∴ ความถี่ของยีน A = ∴ ความถี่ของยีน A = = 0.725 2 = 0.725
= 0.275 และ ความถี่ของยีน a = = 0.275 และ ความถี่ของยีน a =
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p 2 × 200 = (0.275) 2 × 200 110+ (70)
2
200 200 200 200
จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้ จากการค านวณจ านวนต้นที่มีจีโนไทป์ตามกฎฮาร์ดี-ไวน์เบิร์ก ซึ่งค านวณความถี่ของยีนได้ดังนี้
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย 2 2 = (0.275) × 200
2
2
จ านวนต้นที่มีจีโนไทป์ AA ตามค่าที่คาดหมาย = p × 200 = p = (0.275) × 200 × 200