Page 16 -

8
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์

ปกติแต่งงานกันเอง เมื่อทําการสร้างตารางเกี่ยวกับสัดส่วนของการเกิดลูกที่เป็นคนเผือกจะเกิดขึ้น
ดังนี้
คู่ผสมของการแต่งงาน

aa x aa
Aa x aa
Aa x Aa
4
2 2
3
q
4p q
4pq
ความถี่ของจีโนไทป์
2 2
ความถี่ของจีโนไทป์ AA
-
p q
-
3
2 2
ความถี่ของจีโนไทป์ Aa
2p q
2pq
-
2 2
2
2 2
4
3
ความถี่ของจีโนไทป์ aa
p q +2pq + q = q
q
2pq
p q
อัตราส่วนลูก aa เมื่อเทียบกับ
� �
�
�
2pq
q
p q
1
�q
�p
� 2pq
�
�
ลูก aa ที่เกิดขึ้นทั้งหมด
�
�
�
q
q
q
2
กําหนดจีโนไทป์ aa เกิดขึ้น 1 ใน 10,000 คน มีค่าความถี่ของจีโนไทป์ aa;q =0.0001
โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว ผลรวม 4 2
จะได้ค่า q = 0.01 และ p = 0.99
2
(0.01)
จํานวนจีโนไทป์ที่เกิดขึ้นในแต่ (0.99) 2 2(0.99)(0.01) บทที่ 1 องค์ประกอบทางพันธุกรรม 9
1
และการเข้าสู่สมดุลของประชากร
ละคู่ผสม = 0.9801 =0.0198 = 0.0001
จะเห็นได้ว่าคู่ผสม Aa x Aa แสดงการเกิดลูกที่มีจีโนไทป์ aa มากที่สุด
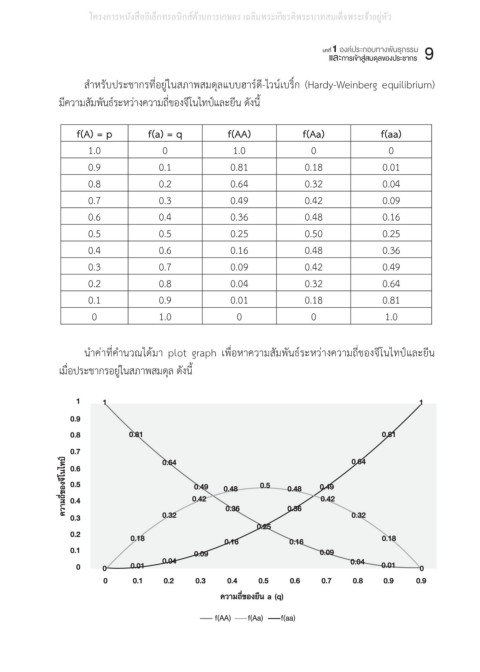
ส�าหรับประชากรที่อยู่ในสภาพสมดุลแบบฮาร์ดี-ไวน์เบริ์ก (Hardy-Weinberg equilibrium)
มีความสัมพันธ์ระหว่างความถี่ของจีโนไทป์และยีน ดังนี้
สําหรับประชากรที่อยู่ในสภาพสมดุลมีความสัมพันธ์ระหว่างความถี่ของจีโนไทป์และยีนดังนี้
f(A) = p f(a) = q f(AA) f(Aa) f(aa)
1.0 0 1.0 0 0
0.9 0.1 0.81 0.18 0.01
0.8 0.2 0.64 0.32 0.04
0.7 0.3 0.49 0.42 0.09
0.6 0.4 0.36 0.48 0.16
0.5 0.5 0.25 0.50 0.25
0.4 0.6 0.16 0.48 0.36
0.3 0.7 0.09 0.42 0.49
0.2 0.8 0.04 0.32 0.64
0.1 0.9 0.01 0.18 0.81
0 1.0 0 0 1.0

นําค่าที่คํานวณได้มา plot graph เพื่อหาความสัมพันธ์ระหว่างความถี่ของจีโนไทป์และยีนเมื่อ
น�าค่าที่ค�านวณได้มา plot graph เพื่อหาความสัมพันธ์ระหว่างความถี่ของจีโนไทป์และยีน
ประชากรอยู่ในสภาพสมดุลดังนี้
เมื่อประชากรอยู่ในสภาพสมดุล ดังนี้