Page 105 -

โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว

98 98 พันธุศาสตร์ประชากร พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
98
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
สำาหรับการปรับปรุงพันธุ์

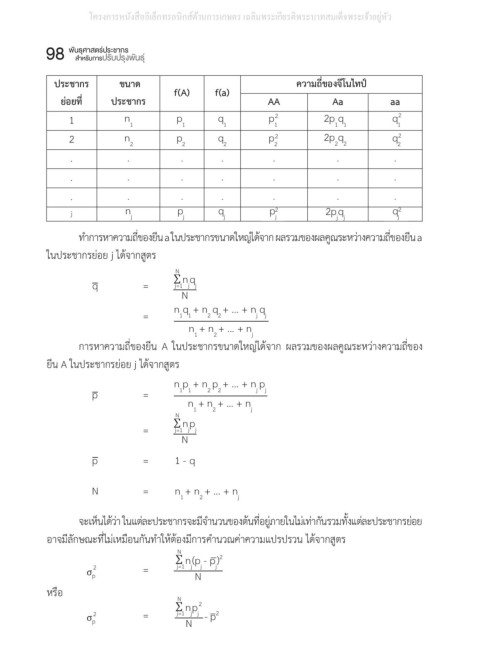
ความถี่ของจีโนไทป์
ประชากร ประชากร ขนาด ขนาด f(A) f(a) ความถี่ของจีโนไทป์
f(A)
f(a)
ย่อยที่ ย่อยที่ ประชากร AA AA Aa Aa aa aa
ประชากร
2 2p q
2 p
n
2 q
q
p
2
2
1 1 n n p p q p p 2p q 2p q q q
2
q
1 1
1 1 1 1
1 1
1 1 1
1
1 1
1 1 1
1
1
1
1
2 2p q
n
2 p
p
q
2 q
2
2 2 n n p p q p p 2p q 2p q q q
2
2
2 2 2
q
2
2 2
2 2
2 2 2
2 2
2 2 2 2
2
2
2
2
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. 98 . . . . . . . . . . .
. พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ .
p
p
q
2 2pq
q
2 2
2 2
j j n jj n p p q q p p 2p q 2p q q q
n
2
j j j
j j j
j j
j
j j
jj
j
j
j
j
j j
ประชากร

92 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ ขนาด f(A) f(a) ความถี่ของจีโนไทป์
ท�าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a

ท าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a ใน
ท าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a ใน
ย่อยที่
ประชากร
ในประชากรย่อย j ได้จากสูตร AA Aa aa
ประชากรย่อย j ได้จากสูตร
ประชากรย่อย j ได้จากสูตร
อิทธิพลของประชากรขนาดเล็ก (genetic drift) n p q p 2p q q
1 จะเห็นได้ว่าการเปลี่ยนแปลงความถี่ของยีนที่เกิดจาก
2
2
92 N 1 N N 1 1 1 1 1 1
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
∑
∑
กลายยีน การอพยพ และการคัดเลือกจะเป็นการคัดเลือกที่เป็นแบบมีทิศทางซึ่งประชากรจะมีขนาดใหญ่ p 2p q q
n q
nq n q

q q̅ 2 =
q̅
= = n
j=1
q
j=1
2
2
j j
p
j j
j j
j=1

2
N N N 2 2 2 2 2 2
.
ในขณะที่ประชากรที่มีขนาดเล็กจะไม่มีทิศทางในการเกิดการเปลี่ยนแปลงความถี่ของยีนซึ่งโอกาสที่ยีนจะ . . .
.
.
.
อิทธิพลของประชากรขนาดเล็ก (genetic drift) จะเห็นได้ว่าการเปลี่ยนแปลงความถี่ของยีนที่เกิดจาก
n q + n q + ⋯ + n q
n q + n q + ⋯ + n q
2 2 j j
1 1

2 2

n q + n q + ... + n q j j
1 1

j j
1 1
=
2 2
==
.
. ที่มีขนาดเล็กนี้
n + n + ⋯ + n .
n +
ปรากฏได้นั้นอาศัยความน่าจะเป็นในการคงอยู่ของยีน ซึ่งประชากร n + ⋯ + n 2 . จะมีจ านวนของประชากร . . .
n + n + ... + n
กลายยีน การอพยพ และการคัดเลือกจะเป็นการคัดเลือกที่เป็นแบบมีทิศทางซึ่งประชากรจะมีขนาดใหญ่
j
2
1
j
98
1
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
j
1
2
การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน A ใน
การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน A ใน
ให้เท่ากับ N เพราะฉะนั้นจ านวนของยีนที่เกิดขึ้นทั้งหมดจะเท่ากับ 2N เนื่องจากยีน 1 ต าแหน่งจะมี 2 อัลลีล . . .
.
.
.
.

การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของ
ในขณะที่ประชากรที่มีขนาดเล็กจะไม่มีทิศทางในการเกิดการเปลี่ยนแปลงความถี่ของยีนซึ่งโอกาสที่ยีนจะ

ประชากรย่อย j ได้จากสูตร
ประชากรย่อย j ได้จากสูตร
และก าหนดให้ยีน a เป็น ค่า q ซึ่งจากประชากรที่มีการผสมกันอย่างสุ่มแล้ว ความถี่ของยีน a p 2p q q
q ในรุ่นลูกจะมี
j
n
p
2
2
ยีน A ในประชากรย่อย j ได้จากสูตร
ประชากร
ขนาด
ปรากฏได้นั้นอาศัยความน่าจะเป็นในการคงอยู่ของยีน ซึ่งประชากรที่มีขนาดเล็กนี้ จะมีจ านวนของประชากร j ความถี่ของจีโนไทป์ j
j
j
j j
j
n p + n p + ⋯ + n p f(a)

โอกาสที่เกิดขึ้นจ านวน 2N+1 ค่า ซึ่งมีการกระจายตัว binomial คือ (a+b) โดยเมื่อความถี่ของยีน A และ a
98
n p + n p +
1 1 2 ⋯ + n p
2 2 f(A) j
AA
j j
j
1 1
2 2
= ประชากร
ย่อยที่ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์

n p + n p + ... + n p
p̅
p̅ =
ให้เท่ากับ N เพราะฉะนั้นจ านวนของยีนที่เกิดขึ้นทั้งหมดจะเท่ากับ 2N เนื่องจากยีน 1 ต าแหน่งจะมี 2 อัลลีล Aa aa
ท าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a ใน
1 1 n + n + ⋯ + n
j j
p = n + n + ⋯ + n 2 2N!
2 2 j
2
j
1
1
2N

1
2
2N−a a
ประชากรย่อย j ได้จากสูตร
แล้วจะมีโอกาสที่เกิดความถี่ของยีน a ในรุ่นลูก คือ a/2N นั่นคือ [ n N n + n + ... + n q p 2N−a a p 2p q q
และก าหนดให้ยีน a เป็น ค่า q ซึ่งจากประชากรที่มีการผสมกันอย่างสุ่มแล้ว ความถี่ของยีน a
q
1ในรุ่นลูกจะมี
p
] p
q =
2
N
1
1
1 1
1
∑ a
(2N−a)!a!
1
n p
ประชากร ∑ j=1 = ขนาด j=1 1 n p 2 j ความถี่ของจีโนไทป์
=
j j
j j
N
2
q
p
N n q โดยเมื่อความถี่ของยีน A และ a
โอกาสที่เกิดขึ้นจ านวน 2N+1 ค่า ซึ่งมีการกระจายตัว binomial คือ (a+b) 2 f(A) f(a) AA 2p q q
2
p
2
N
โดย
n ∑
N
= ประชากร

Aa

= ย่อยที่
aa

2
2 2
2
2
2
q̅
2 np j j
j=1
j j
j=1
p̅ p̅ . = 1 − q 2N . 2N! . . . .
1 − q N
1
= . N 2N−a a
แล้วจะมีโอกาสที่เกิดความถี่ของยีน a ในรุ่นลูก คือ a/2N นั่นคือ [ ] p q = p 2N−a a 2
p
(2N−a)!a!
p = ความถี่ของยีน A N p N . ൌ n + n n n q + n q + ⋯ + n q 1 p 2p q q
q 2
q
a
1 1
1
2 2 1
1
.
.
1
.
.

j j
1 1
ൌ . + ⋯ + n
n + n + ⋯ + n

.
1
= = 2
2
j
1
1 - q 2 j
q
n + n + ⋯ + n
2p q
2p
p
2
jq
2
n
q
โดย = ความถี่ของยีน a จะเห็นได้ว่าในแต่ละประชากรจะมีจ านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อยอาจมี
1
จะเห็นได้ว่าในแต่ละประชากรจะมีจ านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อยอาจมี
.
2
2 2
.
.
2
.
2
.
2
.
.
2
การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน A ใน
.
a = โอกาสที่จะพบยีน a N . = . n + n + ... + n . . . .
ลักษณะที่ไม่เหมือนกันท าให้ต้องมีการค านวณค่าความแปรปรวน ซึ่งคิดได้จากสูตร
j
p
q
n
p
p = ความถี่ของยีน A ลักษณะที่ไม่เหมือนกันท าให้ต้องมีการค านวณค่าความแปรปรวน ซึ่งคิดได้จากสูตร 2p q q
2
2
1
ประชากรย่อย j ได้จากสูตร
j
2
j j
j
j
j
j
j
N = จ านวนต้นในประชากร . N . N . . . . .
= ความถี่ของยีน a
2
q และได้มีการหาความแปรปรวนของความถี่ของยีนในประชากร ซึ่งเป็นผลต่างของค่าความถี่ของยีน a
2
n (p − p̅ )
n (p − p̅ )
j

j
j
j
j
j
จะเห็นได้ว่า ในแต่ละประชากรจะมีจ�านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อย
ท าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a ใน
σ
=
σ =
n p + n p + ⋯ + n p
2
2

∑ 1
.
∑
1
j j
2 2
p
N
N
a = โอกาสที่จะพบยีน a p̅ . p j=1 = . j=1 n + n + ⋯ + n j . . . .
อาจมีลักษณะที่ไม่เหมือนกันท�าให้ต้องมีการค�านวณค่าความแปรปรวน ได้จากสูตร
ประชากรย่อย j ได้จากสูตร
2
1
j
ของแต่ละสายพันธุ์ (q ) กับความถี่ของยีน a ของประชากรเดิม (q) คือ δ = (q − q) ซึ่งหาได้จากสูตร p 2p q q
q
p
n
2
หรือ
หรือ
2
N = จ านวนต้นในประชากร j N ∑ N n p j j j j j j j
q
j
N = N ∑ j=1 n j j 2
2 q - p)
j=1 n(p
N
และได้มีการหาความแปรปรวนของความถี่ของยีนในประชากร ซึ่งเป็นผลต่างของค่าความถี่ของยีน a
2
j j
=
j=1 N j
j
ท าการหาความถี่ของยีน a ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน a ใน
n p j
= q)q
q̅ pq
j j
(1 − n p
2 2
j j
2
σ
2
= − p̅
− p̅
2

p =
2
N
∑
σ = ∑
σ
=
N
p
2N
2N N
p δ q
N
p̅
1 − q
=
ของแต่ละสายพันธุ์ (q ) กับความถี่ของยีน a ของประชากรเดิม (q) คือ δ = (q − q) ซึ่งหาได้จากสูตร
ประชากรย่อย j ได้จากสูตร
j=1
j=1
n q + n q + ⋯ + n q
หรือ
j
และ
และ

=
σ = ค่าความแปรปรวนของผลต่างของความถี่ข องยีน a 1 1 q 2 2 j j j
2
N
j=1 np
1 2 2
n + n + ⋯ + n
δ q N ൌ n + n + ⋯ + n j
1 N
j
2
=
=
q̅
j j
- p
2 2 pq (1 − q)q ∑ n q 2
j=1 j j
p การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน A ในมี

N
σ จะเห็นได้ว่าในแต่ละประชากรจะมีจ านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อยอาจ
=
=
N
ตัวอย่าง ท าการสุ่มเมล็ดพืช 50 เมล็ด จากประชากรขนาดใหญ่ โดยก าหนดให้ความถี่ของยีน a มีค่าเท่ากับ
δ q
2N
2N
ลักษณะที่ไม่เหมือนกันท าให้ต้องมีการค านวณค่าความแปรปรวน ซึ่งคิดได้จากสูตร
n q + n q + ⋯ + n q
2 2
= ค่าความแปรปรวนของผลต่างของความถี่ของยีน a
j j
1
ประชากรย่อย j ได้จากสูตร 1

σ

2
=
0.5 และความถี่ของยีน A เท่ากับ 0.5 แล้วจะพบการกระจายตัวของความถี่ของยีนที่มีค่าความน่าจะเป็นของ
δ q
N n + n + ⋯ + n
j
1
2
2
1 1 n (p − p̅ )
n p + n p + ⋯ + n p
2 2
j j

j
j
j
การกระจายตัวดังนี้ จากสูตตร การหาความถี่ของยีน A ในประชากรขนาดใหญ่ได้จาก ผลรวมของผลคูณระหว่างความถี่ของยีน A ใน
p̅
=

2
σ
= ∑
p
n + n + ⋯ + n
ตัวอย่าง ท าการสุ่มเมล็ดพืช 50 เมล็ด จากประชากรขนาดใหญ่ โดยก าหนดให้ความถี่ของยีน a มีค่าเท่ากับ
N
2
1
j
ประชากรย่อย j ได้จากสูตร
j=1
0.5 และความถี่ของยีน A เท่ากับ 0.5 หรือ pq = ∑ N n p
σ แล้วจะพบการกระจายตัวของความถี่ของยีนที่มีค่าความน่าจะเป็นของ

2
j j
=
j=1
δ q
2N N n p + n p + ⋯ + n p
2 2
N 1
j j
1
2
การกระจา σ = n p 2
p̅
แทนค่า ยตัวดังนี้ จากสูตตร
j j
− p̅
2
=
1 − q
2
1
p̅ p = ∑ n + n + ⋯ + n j
N
σ และ N 0.5 × 0.5 j=1 N n p
pq
2
∑
=
ൌ
δ q
n + n + ⋯ + n
2

=

j j
j=1
=
σ
2(50)
δ q 2N 1 2 j
N
แทนค่า จะเห็นได้ว่าในแต่ละประชากรจะมีจ านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อยอาจมี
=
1 − q
p̅
0.5 × 0.5
σ ลักษณะที่ไม่เหมือนกันท าให้ต้องมีการค านวณค่าความแปรปรวน ซึ่งคิดได้จากสูตร
=

√ 0.5 × 0.5
σ = 2(50)
2
δ q
δ q N ൌ N n + n + ⋯ + n
2 j
2
1
2(50) n (p − p̅ )
j
j
j
σ
=
2

จะเห็นได้ว่าในแต่ละประชากรจะมีจ านวนของต้นที่อยู่ภายในไม่เท่ากันรวมทั้งแต่ละประชากรย่อยอาจมี
∑
p
N
0.5 × 0.5
j=1
σ = ลักษณะที่ไม่เหมือนกันท าให้ต้องมีการค านวณค่าความแปรปรวน ซึ่งคิดได้จากสูตร

√
δ q หรือ 2(50)
N
N n (p − p̅ ) 2
j
σ = ∑ n p 2 j j 2
2
j j
σ = − p̅
2 p
p ∑ N
j=1 N
หรือ j=1
และ
N 2
n p
2
σ = j j − p̅
2
p ∑
N
j=1
และ