Page 108 -

โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว

บทที่ 2 การเปลี่ยนแปลง
ความถี่ของยีน 101 101
บทที่ 2 การเปลี่ยนแปลงความถี่ของยีน

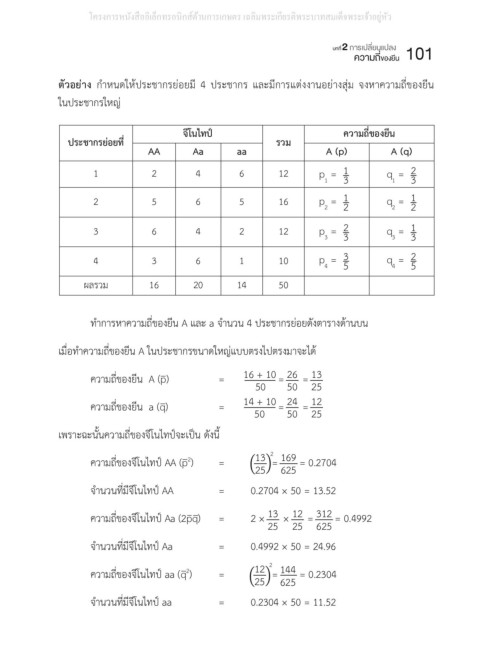
ตัวอย่ำง ก�าหนดให้ประชากรย่อยมี 4 ประชากร และมีการแต่งงานอย่างสุ่ม จงหาความถี่ของยีน
ตัวอย่าง ก าหนดให้ ประชากรย่อยมี 4 ประชากร และมีการแต่งงานอย่างสุ่ม จงหาความถี่ของยีนในประชากร
240
240
ในประชากรใหญ่
ൌ

ใหญ่ 400 = 2 2 2 (20)
× ×240
ความถี่ของยีน
1 1

ประชากรย่อยที่ จีโนไทป์ (110)] 2 1 1 [ (130)− รวม
ൌ
2
2
AA Aa aa A (p) A (q)
1 2 4 6 ( − ) 12 (1) 2 p = 1 1 q = 2
2
ൌ
q =
p =
∴ 
1 1 3 3 1 1 3 3
1
2 5 1 6 2 240 5 = 240 ൌ 16 p = 1 1 q = 1
p =
q =
2
2
2 2
2 2
เท่ากับ 50+60 = 110 แทนค่าสูตร
2

2
1
2
1
6 4 1 400 2 2 2 1 1 2 (20) ൌ 12 p = 2 2 จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค า q = 1
2 ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
q =
p =
3
3
3 3
× ×240
3
3
3 นวณได้ดังนี้
3 3
4 3 6 2 1 2 1 [ (130)− (110)] 10 p = 3 3 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 2 q = 2 2
p =
q =
4 5
4 5
4
5 4 5

1

(1)
ผลรวม -1 60 20 -1 14 ( − ) 50 2 50  ∴ aabb

16 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
ൌ
-1 1 -1 60 aaBb
1
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
-1 ท าการหาความถี่ของยีน A และ a จ านวน 4 ประชากรย่อยดังตารางด้านบน Aabb เท่ากับ 50+60 = 110 แทนค่าสูตร
-1
60
1
2
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
1
2
1
2
ท�าการหาความถี่ของยีน A และ a จ�านวน 4 ประชากรย่อยดังตารางด้านบน ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a
เมื่อท าความถี่ของยีน A ในประชากรขนาดใหญ่แบบตรงไปตรงมาจะได้ 70 AaBb
1
มีค่า
1
1
1
เมื่อท�าความถี่ของยีน A ในประชากรขนาดใหญ่แบบตรงไปตรงมาจะได้ดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
Locus A
Locus B
Linkage
ความถี่ของยีน A (p̅) = 16 + 10 26 13 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 จีโนไทป์
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แส จ านวนต้น
=
=
ความถี่ของยีน A (p) = 50 16 + 10 26 13
= =
50
25
orthogonal
50 25
50
60 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 50 aabb 1
2
จากสูตรที่ 1 
a
n
2
i
= ∑
=
1
-1
12
-1
= =
ความถี่ของยีน a (q) = (n−1) -1 14 + 10 [ = 24 ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ
4
1
2
i

คนละโครโมโซม
4
m i N
50 25
=

5050
50
25
-1
1
14 + 10 24 12 60
3 aaBb
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
แหน่งว่าอยู่
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง
ความถี่ของยีน a (q̅) B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต า
2
2
2
เพราะฉะนั้นความถี่ของจีโนไทป์จะเป็นดังนี้  2 (70) +(60) +(60) +(50) 2ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน Aabb
1
60
-1
-1
เพราะฉะนั้นความถี่ของจีโนไทป์จะเป็น ดังนี้ (1) ൌ ( ) −240
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
(240)
4
2
2
169
169
1
1
AaBb
1

1 70
2
= 0.2704
ความถี่ของจีโนไทป์ AA (p ) = 13 ) = = = 0.2704 243.33 − 240 = 3.33 อยู่บนคนละโครโมโซม
14
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่ง
60
2 = (
25 625 625
) −240 =
13,600ൌ (
25 60 ) −240 =จ านวนต้น จีโนไทป์
Locus B
Linkage
ความถี่ของจีโนไทป์ AA (p̅ ) 243.33−240=3.33
Locus A
14
ൌ (,600
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้

จ านวนที่มีจีโนไทป์ AA
จ�านวนที่มีจีโนไทป์ AA = = 4 1 0.2704 × 50 = 13.52
(240)
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
orthogonal
(1)
) −240
ൌ (
0.2704 × 50 = 13.52 
] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ
2 (70) +(60) +(60) +(50) 2 1
2
2
2
2
จากสูตรที่ 1 
a
13n
ความถี่ของจีโนไทป์ Aa (2pq) = (n−1) = ∑ [ 12 i 13 = 312 = 0.4992 เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
2
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B
=
ความถี่ของจีโนไทป์ Aa (2pq)
2 × × = = 0.4992
3
12 3121
4
2
i
2 ×
คนละโครโมโซม
× m i N
4
4
(n−1)
คนละโครโมโซม 1 25 ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ i 2 25[ a m i N 25 n i 625 = ∑ 25 625 จากสูตรที่ 1  ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต า
3
2
4
จ านวนที่มีจีโนไทป์ Aa
แหน่งว่าอยู่
2
2
2
2
1
จ�านวนที่มีจีโนไทป์ Aa =  2 0.4992 × 50 = 24.96 2ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
0.4992 × 50 = 24.96
(70) +(60) +(60) +(50)
=
(1) ൌ ( 1 ) −240
(240) orthogonal เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
4
2
2
จีโนไทป์
144

ความถี่ของจีโนไทป์ aa (q )
ความถี่ของจีโนไทป์ aa (q̅ 2 = = 12 ) = = = 0.2304 Locus B Linkage
14
= 0.2304
(
60
Locus A = 243.33 − 240 = 3.33

) −240
25 12,600ൌ ( 625 น้อยกว่า 7.815 ที่ df ของตา
625
2 ) จ านวนต้น ) −240=243.33 − 240 = 3.33
25 60
144รางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
14
ൌ (,600

AaBb
1
จ านวนที่มีจีโนไทป์ aa
จ�านวนที่มีจีโนไทป์ aa = 70 1 = 4 0.2304 × 50 = 11.52 หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า 1 1
0.2304 × 50 = 11.52
(240)
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
(1)
Aabb
60
) −240
ൌ (

จากนั้นท าการหาความถี่ที่เปลี่ยนแปลงในลักษณะของแต่ละจีโนไทป์ 2 1 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ -1 -1

(70) +(60) +(60) +(50)
2
2
2
2
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
1
60
-1

4
คนละโครโมโซม 1 50 ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ i 2 a m i N i n = ∑ [ -1 (n−1) -1 2 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ จากสูตรที่ 1  60 -1 1
4
aaBb 23
aabb
1

(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 orthogonal เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
จีโนไทป์ จ านวนต้น
Locus B
Linkage
Locus A
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
AaBb 1 70 2 1 1 1 หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า 1 2 1
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
Aabb
60
เท่ากับ 50+60 = 110 แทนค่าสูตร 2 1 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ -1 -1
aaBb 60 -1 1 -1
50
aabb ∴  2 ( − ) พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 60 -1 1
-1

(1) ൌ

(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
1
1
[ (130)− (110)] 2
ൌ 2 2
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
1 1
× ×240
2 2
400 ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
ก าหนดให้ m และ m และมีค่าเท่ากับ 1
2
(20)
1 2 ൌ = 2 1 2
เท่ากับ 50+60 = 110 แทนค่าสูตร 240 240
∴  2 ( − )

(1) ൌ

1 1 2
[ (130)− (110)]
ൌ 2 1 1 2
× ×240
2 2
2
(20) 400
ൌ =
240 240