Page 35 -

28
โครงการหนังสือ
400อิเล็กทรอน
(20)ิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว
240
240
240
240
240
240

28 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
ൌ
ൌ

ൌ

=
=
=
400
(20)
400
(20)
×240 240 = 2 2 240 240 ൌ = 240 240 ൌ 2 2 = 240 ൌ 2 2
2
2
2
28 พันธุศาสตร์ประชากร 2 2 1 × 1 1400 2 2 1 2 2 2 40 [ (130)− (110)] 2 (20)0 ൌ 2 2 1 × ×240 2 2 (20) 1 1 2 1 [ (130)− (110)] 400 2 1 2 2 2 ൌ × ×240 1 (20) 1 2 1 [ (130)− (110)] ൌ
สำาหรับการปรับปรุงพันธุ์
0.8 2 2 1 2 × ×240 1 1 2 2 1 1 × ×240 2 ൌ [ (130)− (110)] 1 ൌ 1 (1) 2 21 − ) 2 1 ( ൌ ∴ [ (130)− (110)] ൌ × ×240 1 1 2 (1) 1 2 [ (130
0.7 ( − ) (1) (1) ( − ) (1)
0 6 0.6 ( − ) ൌ 2 ( ൌ ∴  2 − ) ( ∴  ൌ 2 เท่ากับ 50+60 = 110 แทนค่าสูตร − ) ∴  เท่ากับ 50+60 = 110 แทนค่าสูตร เท่ากับ 50+60 = 110 แทนค่าสูตร
0.5 2 1 2 1 1 2 1 2 1 2 1 1 2 1 ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า 2 ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า 1 ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
2
2
0 4 0.4 1 2ะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ 1 2รที่ 2 ในการค านวณได้ดังนี้ 1 2 2 1 2 2 จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ 1 เท่ากับ 50+60 = 110 แทนค่าสูตร จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จ เท่ากับ 50+60 = 110 แทนค่าสูตร ก าหนดให้ m และ m จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูต เท่าก
2
2
2
0.3 -1 1 ความถี่ของยีน X a 1 1 1 240 = 1 และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า 240 ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า ൌ ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
0 2 0.2 400 2 (20) จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค
60 60 -1 60 -1 240 50 -1 240 50 aabb ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 -1 50 aabb aabb
0.1 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ (1) ทดสอบอัตราส่วนขอ (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
-1 1
1
× ×240
ൌ

2 2งยีนต าแหน่ง A เป็น 1 : 1
=
(1)
1 1

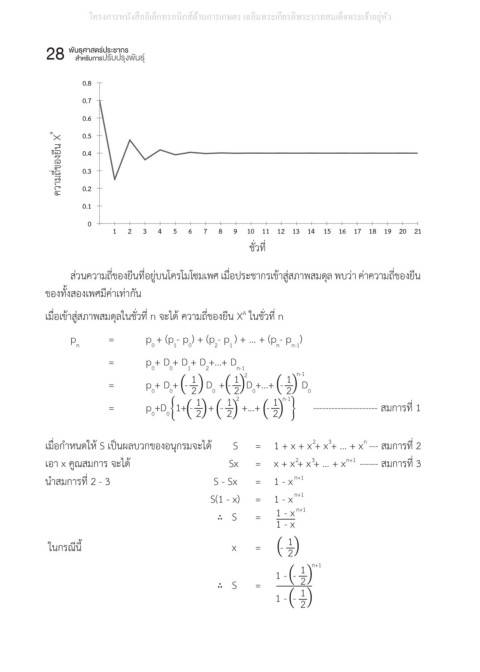
1 -1 -1 ส่วนความถี่ของยีนที่อยู่บนโครโมโซมเพศ เมื่อประชากรเข้าสู่สภาพสมดุล พบว่า ค่าความถี่ของยีนส่วนความถี่ของยีนที่อยู่บนโครโมโซมเพศ เมื่อประชากรเข้าสู่สภาพสมดุล พบว่า ค่าความถี่ของยีน

(20)

400
ൌ

60
60
60
0
2 60 -1
aaBb
-1 1
aaBb 60
-1
aaBb
-1
2 260
1 -1
1 2 3 4 5 6 7 8 9
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 15 16 17 18 19 20 21
400 10 11 12 13 14
2
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
1
1
aabb 50
-1 -1
-1 1
[ (130)− (110)] -1

aabb
240 50
ൌ
1
aabb
-1
240 50
1
2 2 =

ของทั้งสองเพศมีค่าเท่ากัน ของทั้งสองเพศมีค่าเท่ากัน 2 60 -1 × ×240 60 1 1 1 2 ൌ 2 (20) Aabb 60 ൌ aaBb 60 (1) 60 aaBb 60 Aabb aaBb Aabb

ชั่วที่
-1
1 -1
-1 -1
1
-1 -1
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่าหาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่าหาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า

-1
1 -1
-1 1
1
-1
-1
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์

[ (130)−
(110)]
2 2
2
∴ 
1

1 ×240
×
เมื่อเข้าสู่ภาวะสมดุลคือในชั่วที่ n จะได้ ความถี่ของยีน X ในชั่วที่ n
AaBb
70
( − )2 70
1
1 1
1
1
1
AaBb
AaBb 70
1 1
1
1 1
A
A

ൌ
ส่วนความถี่ของยีนที่อยู่บนโครโมโซมเพศ เมื่อประชากรเข้าสู่สภาพสมดุล พบว่า ค่าความถี่ของยีน
-1
1
-1 -1
Aabb
-1
60 1
Aabb 60
1 -1
1 น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซมน้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซมน้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
-1
Aabb 60
2
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่าหาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่าหาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
(1)
ൌ [ (130
เมื่อเข้าสู่ภาวะสมดุลคือในชั่วที่ n จะได้ ความถี่ของยีน X ในชั่วที่ n )− (110)]

Linkage
Locus A
Linkage
Locus A Locus B
Locus B

Locus B
2 Locus A
Linkage
1
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
( − )
70
1
1

AaBb
2 1
AaBb
1 1
1
1
∴  AaBb 70
1
เท่ากับ 50+60 = 110 แทนค่าสูตร ์ 70
จ านวนต้น
จีโนไทป์
จีโนไทป
จีโนไ
จ านวนต้น
1 จ านวนต้น
2ทป์
p น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซมน้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซมน้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม

orthogonal
n Locus B Linkage Linkage 2 Locus B = p 1 0 = Locus A 1 2 0 1 2Locus A 1 0 − n 2 ൌ ) + ⋯ + (p − p n−1 )
orthogonal
orthogonal
1 (1)
0 n
ของทั้งสองเพศมีค่าเท่ากัน p + (p − p ) + (p − p ) + ⋯ + (p − pp + (p − p ) + (p − p )
Linkage
Locus A us B
Loc
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
∴ 
n เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
เมื่อเข้าสู่สภาพสมดุลในชั่วที่ n จะได้ ความถี่ของยีน X ในชั่วที่ n a 2 i 2 ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ

=
p + D + D + D + ⋯ +p
p

2
2
D + D + ⋯ + D
n จีโนไทป์
n−11 จ านวนต้น
1
1
จีโนไทป์
1 ) จ านวนต้น
p + a
a
2 จีโนไทป์
2 ( จ านวนต้น
2
n2
0 2
0
2
n
n−1
0
1 n
n−1
0 n
i
1 i
เท่ากับ 50+60 = 110 แทนค่าสูตร
orthogonal
orthogonal
1 i
i (n−1)
(n−1)
orthogonal
(n−1) = ∑ [ m i N ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ = ∑ [ มีค่าเท่ากับ 70+60 = 130 และ a มีค่า i m i N ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ = ∑ [ 2เท่ากับ ส่วน a m i N 2 2 4 3 และ m 1 42 1 จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะ 3 ก าหนดให้ m 4 4
คนละโครโมโซม
A DD + 2
คนละโครโมโซม
คนละโครโมโซม
จากสูตรที่ 1  จากสูตรที่ 1 จากสูตรที่ 1  12
1
= ใช้สูตรที่ 2 ในการค านวณได้ดังนี้
=
n−12
n p p จากสูตรที่ 1  p 0 2 n = a i 0 i 2 1 2 1 0 n a 2 i 1 n-1 − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ
=
D
1 2
3 1 และมีค่า
1
1
จากสูตรที่ 1  จากสูตรที่ 1 
1
p + (p - p ) + (p - p ) + ... + (p - p ) (− )p a
p + D + (− ) D + (− ) D + ⋯ ++ D + (− ) D + (− )
0 n
2
4 = 110 แทนค่าสูตร
4 เท่ากับ 50+60
0
2
n
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
1 2 − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ = ∑ [
2]
n−1 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
i
(70) +(60) +(60) +(50)(70) +(60) +(60) +(50)(70) +(60) +(60) +(50)

(n−1) (n−1) m i N 0 n 2 1 m i N 2 2 0 2 i m i N ] 0 3 2 2 2 2 2 D D + ⋯ + (− ) จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ 00 2 1 2 4 4 2 ก าหนดให้ m และ m 4 4 0 4
i (n−1)
1ซม
คนละโครโมโ
1คนละโครโมโซม
1 คนละโครโมโซม
2
2
2

ൌ (
n2 2 1 22 และมีค่าเท่ากับ ส่วน a
ൌ (
1 = p + D + D + D +...+ D (240) 1 2 1 2gonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน ൌ ( 2 ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน ) −240 ) −240 3 2 ท าการตรวจสอบด้วยวิธี ortho ) −240
(1)
(1)
(1)
60
1
1
1
1 = ∑ [กับ 70+60 = 130 และ a มีค่า
0 2 2] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ = ∑ [ มีค่าเท่า
2 43 1 ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
(240)
(240)
0
0
2
2
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
n−1 4
4
4
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
1
n-1 1
p = p + D + {1 + (− ) + (− ) + ⋯ + (− )p + D + {1 + (− ) + (− 1 2 2 ท าการตรวจสอบด้วยวิธี 60 1 n−1 } (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
2 1
n-1
-1
2
aabb
1 2
50
 -1
22
1 (40
= (70) +(60) +(60) +(50)(70) +(60) +(60) +(50)(70) +(60) +(60) +(50)
2 2


1พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
2
0 n 2
n
0
-1 = p 1  243.33 − 240 = 3.33 0 ) −240 = 243.33 − 240 = 3.33 0 60 1 ൌ ( 1 (1) 22จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน 2ൌ ( 14,600 ൌ ( 22 ท าการตรวจสอบด้วยวิธี nal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน 2 0 2 ) −240 = 243.33 − 240 = 3.33
ൌ (
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
1 ) −240 ) −240 ) −240
-1 60
} ) + ⋯ + (− )
2
2
60
(1)
)
2orthogonal
2orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
(240) (240)
60 ท าการตรวจสอบด้วยวิธี orthogo
) −240 =
(240)
0
0ൌ
aaBb

14,600ൌ (
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
2  14,600 ) −2=243.33 − 240 = 3.33
ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
2 4 60
2 60
ൌ (600
14,
2
1 p + D + - D + - - D +...+ - D 240 = 3.33 ൌ ( 14,600 ) −240 = 243.33 − −240 = 243.33 − 240 = 3.33 ൌ (,600 4 1 n n-1 14 4 60 50 aabb ทดสอบอัตราส่วนของยีนต (1)
1 -1
(1) -1
1าแหน่ง A เป็น 1 : 1
260
1 n 60 1 4 0 1 1−(− Aabb
14,600
1 )
4
4
× aabb 60
60
-1
p +D 1+ - + - +...+ - --------------------- สมการที่ 1 3.33
0 -1
p -1 − 240 = 3.33 = p + D {p 1 (240) 0 ൌ ( ൌ ( (240) ൌ ( 2 ൌ (
60
0 1−(− ) 60บบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
1−(− (240)
0
0
n ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีนท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีนท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
1
1
2 ) −240 = 243.33 − 240
2 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
-1 1
(1)
(1)
(1)
1 ) 14,600 14,600 -1 ) −240=243.33 − 240 = 3.33
) −240 = 243.33= 3.33
2 ) 60
= ) −240
60
1 ) −240
aaBb
) −240
ൌ (
-1 ൌ (
ൌ (
1 } ) −240 = 243.33 − 240 = AaBb 70 
0 ) −240 ) −240 = 243.33 − 240 = 3.33 ൌ (
1 } p + D { = 243.33 − 240 = 3.33 ൌ (
2
14,600
1  14,600
= 14,600
aabb
50
2
2 2
2 2 0 n 1 หาค่าไคสแควร์แ +(60)+(60)+(50) 4 2 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์

2 (70) +(60) +(60) +(50)
(70)
1−(− 2 +(60) +(60) +(50)
(70)
1
เมื่อ n มีค่าสูงขึ้น จะท าให้ (− ) มีค่าใกล้ 0 เมื่ออยู่ในสภาพสมดุล เมื่อ n มีค่าสูงขึ้น จะท าให้ (− ) มีค่าใกล้ 0 เมื่ออยู่ในสภาพสมดุล aaBb Aabb
22
-1 2
22
-1 2
2
60 2
2
1
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
4
4
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
n

1 (240)
(240)
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีนท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีนท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
(240)
60
1
orthogonal หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
(1)
2
3
1
(1)
n 1
1
เมื่อก�าหนดให้ S เป็นผลบวกของอนุกรมจะได้ S = 1 + x + x + x + ... + x --- สมการที่ 2 AaBb
(1)
60
-1
-1
) −240
) −240
) −240
× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
Locus A
Linkage
1 Locus B
ൌ (
ൌ (
ൌ (

m i N
4
m i N +(60) +(60) +(50) 4
(70) +(60) m i N
2
2
4
คนละโครโมโซม คนละโครโมโซม คนละโครโมโซม 2 − N m , = ∑ [ 2ส่วนค่า m 2 ] i 2 a 2 n 1 ∑ [ 2 = N ส่วนค่า m , ] − 2 a 2i จากสูตรที่ 1  n = ∑ 2 n+1ยีนทั้ง 2 ต าแหน่งว่าอยู่ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
(n−1)
22 +(60) +(50)
จ านวนต้น 
(n−1)
i (70)

i
i

4
2
] − N ส่วนค่า m , m 2 4
2
3
2 4
1
1
3
2 1
(n−1) (70) +(60) +(60) +(50) 3
จีโนไทป์
2 2
n 60 จากสูตรที่ 1  [
70
2 1
1
1
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบต าแหน่ง A เป็น 1 : 1 (2) ทต าแหน่ง A
1−0ดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีน
i
n
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
2
Aabb จากสูตรที่ 1 
a
1
1
1
2 2 m และ m มีค่าเท่ากับ
-1 2 2 , m , m และ m มีค่าเท่ากับ
-1 , m และ m มีค่าเท่ากับ
2
1−0
p + D {p หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
Locus A
Locus B
Linkage
4
4
4
m i N
m i N
(n−1) m i N
คนละโครโมโซม คนละโครโมโซม คนละโครโมโซม
เอา x คูณสมการ จะได้ Sx = x + x + x + ... + x ------ สมการที่ 3จีโนไทป์ จ านวนต้น (n−1)
1 } (n−1)
4
i 1
3
2
i
2
2 4
2
orthogonal orthogonal orthogonal
13
S - Sx
n+1
3 4
น�าสมการที่ 2 - 3 Linkage จ านวนต้น เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ 1
1
= 1 - x ] − N ส่วนค่า m , m , m และ m มีค่าเท่ากับ
i
AaBb
1
1
1
3ต าแหน่ง 70
2
จากสูตรที่ 1 
a
] −
จากสูตรที่ 1 [
1 } = [N ส่วนค่า m และ m
= ∑
p + D { ] −N ส่วนค่า m , m , m
0 = ∑ [
0 = ∑ ] −
i
i
i
(n−1)ตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
น้อยกว่า 7.815 ที่ df ของ
n
n
2
2 n
= ∑ [
a
1+ a
จากสูตรที่ 1 
จีโนไทป์ จีโนไทป์
1
a
1
จากสูตรที่ 1
= ,m , m และ
0N ส่วนค่า m มีค่าเท่ากับ
1
n m มีค่าเท่ากับ
p
2
3
1
2
i
2
2 2
0 n ,m , m และ m มีค่าเท่ากับ
4
2เอง เมื่อท าการวิเคราะห์แบบ
เดียวกันหรือไม่มี linkage นั่น
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
คนละโครโมโซม เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห
i orthogonal จะเป็นดังนี้
m i N
4
1+์แบบ orthogonal จะเป็นดังนี้
orthogonal
0 Locus A Locus A
Lo
Linkage Linkage Locus B
n+1
p = จะเป็นดังนี้ p + D = orthogonal ราะห์แบบ orthogonal จะเป็นดังนี้ จ านวนต้น งไคสแควร์เท่ากับว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม p + D orthogonal orthogonal orthogonal เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ จีโนไทป์ น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีน3 แสดงให้เห็น Linkag
0 p
S(1 - x) = 1 - x
2
n Locus A
Locus B
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท า
0
aการวิเคราะห์แบบ orthogonal จะเป็นดังนี้
n
n
3
3
2
จ านวนต้น
1
2 จ านวนต้น จีโนไทป์ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
2ต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่แหน่งอยู่บนคนละโครโมโซม
น้อยกว่า 7.815 ที่ df ของตารา
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต า
n
.
จ านวนต้น จ านวนต้น จีโนไทป์
2
2
n+1 2 i
1
1
= ∑ [
1
จีโนไทป์ จีโนไทป์ 2 จากสูตรที่ 1 ดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดต .. 70 2 ൌ ( (70) +(60) +(60) +(50) m , m และ m มีค่าเท่ากับ
Locus B Locus B cus A เดียวกันหรือไม่มี linkage นั่น
เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเค
2
3
4
1
0เอง เมื่อท าการวิเคราะห์แบบ orthogonal
i
2 (n−1)
คนละโครโมโซม
4
Locus A Locus A
1 - x
p AaBb ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม = p + (p − p ) จ านวนต้น ไคสแควร์เท่ากับ 3 แสดงให้เ p + (p − p ) Locus A น้อยกว่า 7.815 ที่ df ) −240 Linkage
0 p
0 =
(1)
1
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่
2ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีนารางไคสแควร์ที่ 0.05 พบว่า มีค่า
] − N ส่วนค่า m , หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
(240)
หาค่าไคสแควร์แบบวิธีเากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
n
n
1
-1
1
-1
3 Aabb 0 3 2 1 0 n a 2 i 4 Locus B Locus B ซม -1 m , m และ m มีค่าเท่ากับ
60 จากสูตรที่ 1 
= เท่ากับ 3 แสดงให้เ
1 น้อยกว่า 7.815 ที่ df ของต
70 แสดงให้เห็นว่า
S 2 1 70 AaBb ห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
1 - x m i Nารางไคสแควร์
AaBb ็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
1 1 น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 ห
1 ของตาราง
1 60 = ∑ [
1 ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
AaBb AaBb 70 1 (n−1) 1 1 m i N × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ 1 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ 2 1 2 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ -1 4 1 4
i

Linkage Linkage Locus B คนละโครโมโ
14,600ൌ ( (70) +(60) +(60) +(50)
2
ในกรณีนี้ = aaBb 0 p 2 1 aaBb 0 = 70 = 243.33 60 -1  (1 ) −240 2 ൌ ( ൌ ( 14 ) −240 = 243.33 − 240 = 3.33 -1 -1

p + p − p -1 60
-1
1
1
p aaBb
60
) −240
x 2
2
= -,600)
p + p − p
1
] − N ส่วนค่า m ,สแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่
1 60 าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ
3 หาค่าไค
Aabb อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
Aabb 3.33 ซึ่งเมื่
2วร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่
หาค่าไคสแค
60 งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
-1 -1
-1 1 2ด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
-1
Aabb Aabb
70 AaBb −240=3.33
60 Aabb
-1 2ท าการตรวจสอบ
0
1
n
n
1
1 ต าแห
1
1 1 น่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
4
2
2
) −240 
n+1
-1 1
-1
aabb aabb 50 60 aaBb 3ธุ์ 60 -1 50 3 1 4นธุ์ (240) 1 = 243.33 − 240 = 3.33 2 -1 ൌ (600 1 - - 60 (70) +(60) +(60) +(50) 60 -1 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 1 ) −240 1 -1 1
aabb
ൌ (
60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
02 60 ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
× aabb
1 -1 (240)× aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
aaBb aaBb
-1
60
(1)
3 1 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
3 60
-1 1 = 3.33
-1 -1  1

-1 พันธุศาสตร์ประชากรกับการปรับปรุงพั
1 พันธุศาสตร์ประชากรกับการปรับปรุงพัน
-1 2ด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
(1)
1 (240)
2ท าการตรวจสอบ 60
60
..
50 ) −240
S -1 )+(60) +(50) 2 = (70) +(60 14, -1 ) −240 = พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ . 1 243.33 − 240 -1
ൌ ( 14,600ൌ (

4

2
aabb (1)
1
(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 -1 aabb ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 60 -1 60 1 -1 1 1
-1
2
2
50 aabb
50
-1
50
2

ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
m i N ൌ (600 1 - -
60
4
) −240 = 243.33 − 240 = 3.33
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
) −240
2 60 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
ท าการตรวจสอบด้วยวิธี orthogonal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
60
) −240

14,600ൌ (
(240) = 243.33 − 240 = 3.33
1
-1 (1)
i (70 2 60
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
4
ൌ ( 14,
คนละโครโมโซม
2
(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 (1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1 (n−1) 2 2  จากสูตรที่ 1 
4
2
3
1
= ∑ [) +(60) +(60) +(50)
] − N ส่วนค่า m , m , m
2
2
i 2
4
n
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบ
1อัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
a
1
และ m มีค่า

เท่ากับ
2
(240)
inal จะทดสอบสมมติฐานดังนี้ (1) ทดสอบอัตราส่วนของยีน
2 ท าการตรวจสอบด้วยวิธี orthogo
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่าก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่าก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
1
1
1
(1)
2็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ บ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้ จะเห็นได้ว่ามีการแบ่งกลุ่มออกเปจะเห็นได้ว่ามีการแ
) −240
ൌ (

2
2
1
2
4

m i N +(60) +(60) +(50)
(70)
คนละโครโมโซม
2
2
(n−1)
1 2
2
2
2
4
3
ต าแหน่ง A เป็น 1 : 1 (2) ทดสอบอัตราส่วนของยีนต าแหน่ง B เป็น 1 : 1 (3) ทดสอบยีนทั้ง 2 ต าแหน่งว่าอยู่
เท่ากับ 50+60 = 110 แทนค่าสูตร เท่ากับ 50+60 = 110 แทนค่าสูตร เท่ากับ 50+60 = 110 แทนค่าสูตร ] − i 2 a 1ง เมื่อท าการวิเคราะห์แบบ m , m n = 2 1linkage นั่นเอ ∑ [ orthogonal เดียวกันหรือไม่มี
12 N ส่วนค่า m ,
จ านวนต้น
2 จากสูตรที่ 1 
1
2orthogonal จะเป็นดังนี้
2 1 และ m มีค่า
1เท่ากับ
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
1
1
1
2 Linkage
2 Locus B
2
1
1
2
2
1
1
1
2 1
m i N
4
คนละโครโมโซม
(n−1)
2
2
i
2
4
น้อยกว่า 7.815 ที่ df ของตารางไคสแควร์เท่ากับ 3 แสดงให้เห็น 3
1
= ∑ [
] − N ส่วนค่า m , m
จีโนไทป์ ว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
เท่ากับ 50+60 = 110 แทนค่าสูตร เท่ากับ 50+60 = 110 แทนค่าสูตร เท่ากับ 50+60 = 110 แทนค่าสูตร i 2 a n 2 Locus A 2 orthogonal เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ 1
จากสูตรที่ 1 
1
70
1
AaBb
( − )( − )( − ) 1
ก าหนดให้ ก าหนดให้ ,m และ m มีค่าเท่ากับ
จีโนไทป
จ านวนต้น

∴ 
∴  2 ∴  2 2 หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า

(1) ൌ ์ ว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม (1) ൌ ൌ ควร์เท่ากับ 3 แสดงให้เห็น Locus A Locus B Linkage
(1)
-1
Aabb 60 1 orthogonal เดียวกันหรือไม่มี linkage นั่นเอง เมื่อท าการวิเคราะห์แบบ orthogonal จะเป็นดังนี้ -1

จีโนไทป์
น้อยกว่า 7.815 ที่ df ของตารางไคสแ
∴  ∴  AaBb 2 1 70 1 ค่าเท่ากั 2 ค่าไคสแควร์มี 2 1 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ หาค่าไคสแควร์แบบวิธีเดิม พบ 1 1
2
2

1 ( − )( − )( − ) 1
Locus A

-1
1
2 2 60
2 -1

ൌ
ൌ
[ (130)− (110)] ൌ
(1)
(1) aaBb 2 ∴  [ (130)− (110)][ (130)− (110)] กว่า 7.815 ที่ df ของตารางไ Locus B Linkage
(1)
2
2
บ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า
ൌ
Aabb ൌ -1 -1
× ×240 60

× ×240 1

1 จ านวนต้น บ 3 แสดงให้เห็นว่า ยีนทั้ง 2 ต าแหน่งอยู่บนคนละโครโมโซม
2 1เท่ากั
คสแควร์
น้อย
1 1
1 1
1 70
AaBb
2 1
× ×240
50
aabb [ (130)− (110)][ (130)− (110)][ (130)− (110)] -1 ทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 6 พันธุศาสตร์ประชากรกับการปรับป 60 × aabb ได้ลูกที่มีจีโนไ หาค่าไคสแควร์แบบวิธีเดิม พบค่าไคสแควร์มีค่าเท่ากับ 3.33 ซึ่งเมื่อเปิดตารางไคสแควร์ที่ 0.05 พบว่า มีค่า 1 1 1
1
1
2 2 1
1
1
2 2
2
2 2 2
1 1รุงพันธุ์
ൌ 0 : 60 : 50 ต้น เมื่อท าการวิเคราะห์
1
2 60
aaBb
2
2
2
2
-1
Aabb
1
ൌ 2 2 ൌ 400 1 1 ൌ 400(20) 2 2 400 -1 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 60 -1 -1 -1
(20)
1 1
1 1 (20)
2ัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
× ×240
(1) ทดสอบอ × ×240× ×240 2 2 = 240 -1 60 × aabb ได้ลูกที่มีจีโนไทป์ AaBb : Aabb : aaBb : aabb เท่ากับ 70 : 60 : 60 : 50 ต้น เมื่อท าการวิเคราะห์ -1 -1
2 2= ൌ
ൌ
= 2 ൌ

240240 50
aabb
1
240
1
-1
240240
2 60
aaBb
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
400(20)
400)

ൌ (20) 2 = (20 =ൌ 2 = 400 -1 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ 60 -1 1
(1) ทดสอบอัตราส่วนของยีนต
240240าแหน่ง A เป็น 1 : 1
2400 50
ൌ
aabb
240
240
24
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
1

จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
2
1
2
1
2
(1) ทดสอบอัตราส่วนของยีนต าแหน่ง A เป็น 1 : 1
เท่ากับ 50+60 = 110 แทนค่าสูตร
ก าหนดให้ m และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
1
จะเห็นได้ว่ามีการแบ่งกลุ่มออกเป็น 2 กลุ่ม สามารถที่จะใช้สูตรที่ 2 ในการค านวณได้ดังนี้
2
1
2 1 2
เท่ากับ 50+60 = 110 แทนค่าสูตร
∴  และ m และมีค่าเท่ากับ ส่วน a มีค่าเท่ากับ 70+60 = 130 และ a มีค่า
( − ) 1
2
ก าหนดให้ m 1 (1) ൌ 2 2
1
2

เท่ากับ 50+60 = 110 แทนค่าสูตร
1
1
( − )
∴  2 [ (130)− (110)] 2

2
2
(1) ൌ ൌ

1 1
× ×240
∴  2 ( − ) 2
1
2 2
1
(1) ൌ [ (130)− (110)]
2
400

ൌ 2 2

(20)
1 1
ൌ 1 = × ×240

1
240
2 2
240 [ (130)− (110)] 2
ൌ 2 2
(20) 2 1 1 400
ൌ 2 × ×240
= 2
240 240
2
(20) 400
ൌ =
240 240