Page 26 -

โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว
17
17
บทที่ 1 องค์ประกอบทางพันธุกรรมและการเข้าสู่สมดุลของประชากร บทที่ 1 องค์ประกอบทางพันธุกรรมและการเข้าสู่สมดุลของประชากร

และการเข้าสู่สมดุลของประชากร 19
ก่อนปรับค่า ก่อนปรับค่า บทที่ 1 องค์ประกอบทางพันธุกรรม
1 − (p + p + p ) 1 − (p + p + p = ) d = d
O
O B
A
B A
ตรวจสอบการค�านวณโดยการรวมค่าความถี่ของแต่ละหมู่เลือดในประชากรซึ่งจะได้ผลรวมเท่ากับ 1
หลังปรับค่า หลังปรับค่า
1 1
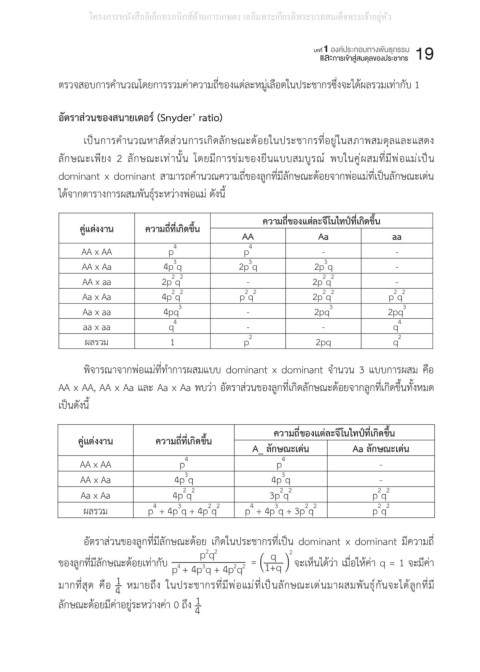
อัตรำส่วนของสนำยเดอร์ (Snyder’ ratio)
d
′ ′ ′ ′ ′ ′ 2 2
1 − (p + p + p ) 1 − (p + p + p = ) = d
18
A B A O B O 4 4
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
18 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
เป็นการค�านวณหาสัดส่วนการเกิดลักษณะด้อยในประชากรที่อยู่ในสภาพสมดุลและแสดง
ตัวอย่าง ก าหนดให้ หมู่บ้านหนึ่งมีจ านวนคนทั้งหมด 200 คน ประกอบด้วยคนหมู่เลือด A 60 คน หมู่เลือด B ตัวอย่าง ก าหนดให้ หมู่บ้านหนึ่งมีจ านวนคนทั้งหมด 200 คน ประกอบด้วยคนหมู่เลือด A 60 คน หมู่เลือด B
เป็นการคํานวณหาสัดส่วนการเกิดลักษณะด้อยในประชากรที่อยู่ในสภาพสมดุลและแสดงลักษณะ
ลักษณะเพียง 2 ลักษณะเท่านั้น โดยมีการข่มของยีนแบบสมบูรณ์ พบในคู่ผสมที่มีพ่อแม่เป็นะ
เป็นการคํานวณหาสัดส่วนการเกิดลักษณะด้อยในประชากรที่อยู่ในสภาพสมดุลและแสดงลักษณ
เพียง 2 ลักษณะเท่านั้น โดยยีนเดียวที่ควบคุมลักษณะที่ปรากฏเพียง 2 ลักษณะหรือมีการข่มแบบสมบูรณ์ พบ
30 คน หมู่เลือด AB 60 คน และหมู่เลือด O 50 คน เมื่อประชากรอยู่ในสมดุลความถี่ของแต่ละหมู่เลือดใน30 คน หมู่เลือด AB 60 คน และหมู่เลือด O 50 คน เมื่อประชากรอยู่ในสมดุลความถี่ของแต่ละหมู่เลือดใน
เพียง 2 ลักษณะเท่านั้น โดยยีนเดียวที่ควบคุมลักษณะที่ปรากฏเพียง 2 ลักษณะหรือมีการข่มแบบสมบูรณ์ พบ
dominant x dominant สามารถค�านวณความถี่ของลูกที่มีลักษณะด้อยจากพ่อแม่ที่เป็นลักษณะเด่น
ในคู่ผสมที่มีพ่อแม่เป็น dominant x dominant สามารถคํานวณความถี่ของลูกที่มีลักษณะด้อยจากพ่อแม่ที่
หมู่บ้านนี้จะเป็นอย่างไร หมู่บ้านนี้จะเป็นอย่างไร
ในคู่ผสมที่มีพ่อแม่เป็น dominant x dominant สามารถคํานวณความถี่ของลูกที่มีลักษณะด้อยจากพ่อแม่ที่
ได้จากตารางการผสมพันธุ์ระหว่างพ่อแม่ ดังนี้
เป็นลักษณะเด่นได้จากตารางการผสมพันธุ์ระหว่างพ่อแม่ดังนี้
เป็นลักษณะเด่นได้จากตารางการผสมพันธุ์ระหว่างพ่อแม่ดังนี้
=
p = p √p̅̅̅̅ √p̅̅̅̅
O O O O ความถี่ของแต่ละจีโนไทป์ที่เกิดขึ้น
คู่แต่งงาน ความถี่ที่เกิดขึ้น ความถี่ของแต่ละจีโนไทป์ที่เกิดขึ้น
50
50
คู่แต่งงาน O = p ความถี่ที่เกิดขึ้น AA Aa aa
p
√ =
√
O
AA x AA p 4 200 200 p 4 AA - Aa - aa
4
4
3 p
p
-
AA x AA = 0.5 = 0.5 2p q 2p q - -
3
3
4p q
AA x Aa
3
2 2+ p̅̅̅̅ − √p̅̅̅̅ p̅̅̅̅ + p̅̅̅̅ − √p̅̅̅̅ q
2 2 2p q
=
AA x Aa p = p 4p q √ O A O O 2p 3 O 2p q 3 - -
2p q
√p̅̅̅̅
AA x aa
-
A
A
A
2 2
2 2
60 q
AA x aa 2p 2 2 50 - 2p q 2 2 -
2 2
2 2
Aa x Aa = 4p q + √ 6 500 −0.5 + p q 2p q p q
√ =
−0.5
2 2
2 2
2 2
2 2
p q
4p q
2p q
Aa x Aa 4pq 2 20000 200 p q 2pq 2pq
3
3
-
Aa x aa
20
30
= 3 0.74 − 0.5 3 3
2pq
4pq
Aa x aa 0.74= 4 − 0.5 - - 2pq q
4
q
-
aa x aa
4
q
aa x aa p = p 0.24 = 4 0.24 p 2 - 2pq - q q
2
ผลรวม
1
A
A
2
2
p
ผลรวม p = p √p̅̅̅ + p̅̅̅̅ − √p̅̅̅̅ p̅̅̅ + p̅̅̅̅ − √p̅̅̅̅ 2pq q
1
=
√
B
B
O B
B
O O
O
พิจารณาจากพ่อแม่ที่ทําการผสมแบบdominant x dominantจํานวน3 แบบการผสม คือ AA x
พิจารณาจากพ่อแม่ที่ท�าการผสมแบบ dominant x dominant จ�านวน 3 แบบการผสม คือ

3
500
50
30
พิจารณาจากพ่อแม่ที่ทําการผสมแบบdominant x dominantจํานวน3 แบบการผสม คือ AA x
−0.5
√ =
=
−0.5 +
+ √
AA x AA, AA x Aa และ Aa x Aa พบว่า อัตราส่วนของลูกที่เกิดลักษณะด้อยจากลูกที่เกิดขึ้นทั้งหมด
2
200
200
20000
AA,AA x Aa และAa x Aaพบว่า อัตราส่วนของลูกที่เกิดลักษณะด้อยจากลูกที่เกิดขึ้นทั้งหมดเป็นดังนี้
AA,AA x Aa และAa x Aaพบว่า 0.63 − 0.5
=
เป็นดังนี้ 0.63 − 0.5 = อัตราส่วนของลูกที่เกิดลักษณะด้อยจากลูกที่เกิดขึ้นทั้งหมดเป็นดังนี้
ความถี่ของแต่ละจีโนไทป์ที่เกิดขึ้น
0.13 =
คู่แต่งงาน p = p ความถี่ที่เกิดขึ้น A_ ลักษณะเด่น Aa ลักษณะเด่น
0.13

B
B
4 (p + p + p ) 1 − (p + p + p ) ความถี่ของแต่ละจีโนไทป์ที่เกิดขึ้น
1 − =
AA x AA
p
คู่แต่งงาน d = d ความถี่ที่เกิดขึ้น B A O B O p 4 -
A
A_ ลักษณะเด่น
3
3
4p q
=
AA x Aa d = d 1 − (0.24 + 0.13 + 0.5) 1 − (0.24 + 0.13 + 0.5) Aa ลักษณะเด่น
-
4p q
4
4
-
p
2 2
2 2
2 2
Aa x Aa
AA x AA = 1 − 0.87 = p 3p q p q
4p q 1 − 0.87
3
3
4p q
4
2 2
AA x Aa p +4p q+4p q p +4p q+3p q p q -
4
4p q
2 2
3
3
2 2
ผลรวม
= 0.13 = 2 2 0.13 2 2 2 2
Aa x Aa 4p q 3p q p q

ท าการปรับค่า ท าการปรับค่า ผลรวม p + 4p q + 4p q p + 4p q + 3p q p q
3
2 2
2 2
4
2 2
4
3
อัตราส่วนของลูกที่มีลักษณะด้อย เกิดในประชากรที่เป็น dominant x dominantมีความถี่ของลูกที่
′ ′ ୮ ୯ 1 1 1 ୯ ଶ 1 ଵ
మ మ
p p
=
(p + d) (1 + d) (p + d) (1 + d)
=
ቁ จะเห็นได้ว่าเมื่อให้ค่า q = 1 จะมีค่ามากที่สุดคือ
ൌቀ
มีลักษณะด้อย เท่ากับ ୮ ାସ୮ ୯ାସ୮ ୯ เกิดในประชากรที่เป็น dominant x dominant มีความถี่
O
O
O
O
อัตราส่วนของลูกที่มีลักษณะด้อย
อัตราส่วนของลูกที่มีลักษณะด้อย เกิดในประชากรที่เป็น dominant x dominantมีความถี่ของลูกที่
2
2
2
2
ర
మ మ
య
ସ
ଵା୯
2 2 2
ଶ
మ మ
q 1
୮ ୯
หมายถึงในประชากรที่มีพ่อแม่ที่เป็นลักษณะเด่นมาผสมพันธุ์กันจะได้ลูกที่มีลักษณะด้อยมีค่าอยู่ระหว่างค่า 0 ଵ
୯
p q 1
1
ของลูกที่มีลักษณะด้อยเท่ากับ จะเห็นได้ว่า เมื่อให้ค่า q = 1 จะมีค่า
1
=
= + (0.13))
=
มีลักษณะด้อย เท่ากับ
2 2ቁ จะเห็นได้ว่าเมื่อให้ค่า q = 1 จะมีค่ามากที่สุดคือ
(0.5 + (0.13))(1 + (0.13)) (0.5 + (0.13))(1
p + 4p q + 4p q
4
3 ൌቀ
2
ถึง ୮ ାସ୮ ୯ାସ୮ ୯ 2 ଵା୯ 2 1+q2 ସ
ଵ

య
మ మ
ర
1
มากที่สุด คือ หมายถึง ในประชากรที่มีพ่อแม่ที่เป็นลักษณะเด่นมาผสมพันธุ์กันจะได้ลูกที่มี
หมายถึงในประชากรที่มีพ่อแม่ที่เป็นลักษณะเด่นมาผสมพันธุ์กันจะได้ลูกที่มีลักษณะด้อยมีค่าอยู่ระหว่างค่า 0
ସ
4
อีกแบบที่พบคือเมื่อพ่อแม่ที่ทําการผสมเป็น dominant x recessive พบว่า อัตราส่วนของลูกที่เกิด
ลักษณะด้อยมีค่าอยู่ระหว่างค่า 0 ถึง 1
ถึง
ଵ
4
ลักษณะด้อยจากลูกที่เกิดขึ้นทั้งหมดเป็นดังนี้ ซึ่งกรณีนี้จะเกิดเพียง 2 แบบการผสมคือ AA x aa และAa x aa
ସ
อีกแบบที่พบคือเมื่อพ่อแม่ที่ทําการผสมเป็น dominant x recessive พบว่า อัตราส่วนของลูกที่เกิด
ความถี่ของแต่ละจีโนไทป์ที่เกิดขึ้น
คู่แต่งงาน
ความถี่ที่เกิดขึ้น
ลักษณะด้อยจากลูกที่เกิดขึ้นทั้งหมดเป็นดังนี้ ซึ่งกรณีนี้จะเกิดเพียง 2 แบบการผสมคือ AA x aa และAa x aa
A_ ลักษณะเด่น
aa ลักษณะด้อย
2 2
2 2
AA x aa 2p q 2p q -