Page 135 -

โครงการหนังสืออิเล็กทรอนิกส์ด้านการเกษตร เฉลิมพระเกียรติพระบาทสมเด็จพระเจ้าอยู่หัว

128 พันธุศาสตร์ประชากร
128
128 สำาหรับการปรับปรุงพันธุ์
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์

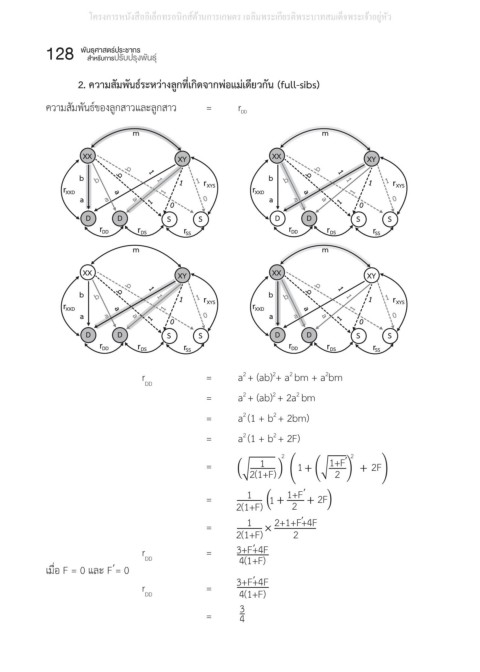
128 ความสัมพันธ์ระหว่างลูกที่เกิดจากพ่อแม่เดียวกัน (full-sibs)
2. ควำมสัมพันธ์ระหว่ำงลูกที่เกิดจำกพ่อแม่เดียวกัน (full-sibs)
2.
2. ความสัมพันธ์ระหว่างลูกที่เกิดจากพ่อแม่เดียวกัน (full-sibs)
พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์
ความสัมพันธ์ของลูกสาวและลูกสาว = r DD
ความสัมพันธ์ของลูกสาวและลูกสาว
ความสัมพันธ์ของลูกสาวและลูกสาว

= =
DD
2. ความสัมพันธ์ระหว่างลูกที่เกิดจากพ่อแม่เดียวกัน (full-sibs)
r r
DD
ความสัมพันธ์ของลูกสาวและลูกสาว = r DD
134 พันธุศาสตร์ประชากรกับการปรับปรุงพันธุ์ ระชากรกับการปรับปรุงพันธุ์ พันธุศาสตร์ป 134

2 m b′) m = ) m + (a′ 2 (a′b′) + (a′b′) + (a′b′) m + (a′b′) m m = a′b′) + (a′b′) +(a′b′ 2 2 2 2 ( 2 2

= 2(a b ) + 2(a′b′) m 2(ab)+2(a′b′)m 2 ′ ′ 2 ′ ′ 2 2 =

m = 2a′ (b + b m ) 2a′(b+bm) 2′ ′ 2 ′ 2 ′ 2 ′ 2 ′2 = m

จากสูตร m′ = F ′ ′ F = จากสูตร m′
b ′ 2 2 ′ b
F′ = m′b′ 2 m′b′ = F′
2
แทนค่า แทนค่า
m = 2a′ (b + F′) (b+F′) ′ 2 ′ 2 2 2a′ = m
2
จาก จาก
r = a + (ab) + a bm + a bm
2
2
2
2
DD 2 2 2 2 1 2 2 1 2 2
a + (ab) + a bm + a bm
2
a′
a + (ab) + a bm + a bm

r r DD = = = = 2 + (ab) + 2a bm 2(1+F ) √ = a′
a
2
DD
√
′
′
2(1+F )
= = a + (ab) + 2a bm
2 2
2 2
2 2
a + (ab) + 2a bm
2
= a 2 (1 + b + 2bm) ′′

2 2 ′′
2 2
1+F
2

r b′ = = a + (ab) + a bm 2 1+F = b′
a (1 + b + 2bm) + a bm
2
2
√
DD = = (1 + b + 2bm) √
a
แทนค่า = = = a + (ab) 2 2 2 2 2 2 แทนค่า
2

2
2 a =
(1 + b +
2+ 2F) 2a bm
2
a (1 + b + 2F)

a (1 + b + 2F)
= a (1 + b + 2bm) , 2 2 2
2 2
2
2
2
= = m = 1 ′ 2 ′ 1 ′ ′ 2 2 1+F ′ = 2F m
1+F 1+F ′
1 1 2
) (1 + (√
2(1+F)
(√
) + 2F)
= (√ 2a′ (b + F ) (b+F) ) (1 + (√ 2 2 2 2a′ ) + 2F)
2
2(1+F) 2
2(1+F)
a (1 + b + 2F)
=
2 2 2 , 2 2 2
1+F
′
= = = = ) + F′] ′′ = 1 1 1 1+F 2(1+F) ) (1 + (√) 2 ′ 1+F ′′ ) + F′]
1
1+F 1 ′
=
1+F
1+F
1
(1 + )×[(√
)
2F ×
1 (√
2
+ 2F) [(√ 2(√
(1 +
′ + 2F
2(1+F)
) + 2F)
(√
′
2(1
2(1+F
2(1+F)
2
2 2 )+F)
2
2(1+F)
2
,
= = 1 1 1 2+1+F+4F
′ ′
2+1+F +4F
2+1+F +4F
′
=

= 2(1+F) × ′′ × 1+F +2F 1+F × 1+F +2F ′ =
′′
1 ′
1
1
2 + 2F)
2(1+F) 2 ×
=
2(1+F)
2(1+F) (1 + 2 2
2 ×
×
′ ,
2 ′′
2(1+F )F)
r DD r r DD = = = 3+F+4F 2 2+1+F +4F 2(1+ 2
′
3+F +4F
3+F +4F
4(1+F)
′
1
DD
4(1+F)
,
4(1+F)
×

เมื่อ F = 0 และ F = 0 m = = , 1+F +2F 2 ′ ′ ′′ 1+F +2F = m
2(1+F)
′′
เมื่อ ൌ Ͳ และ F’= 0
เมื่อ ൌ Ͳ และ F’= 0

′
r r = = 3+F+4F 2(1+F ) ′ 2(1+F )
3+F +4F
′

4(1+F)
′ ′
DD DD 3+F +4F
4(1+F)
3+F +4F
r r DD = = 4(1+F) 2 2 ท าการหาอัตราเลือดชิด (F)
ท าการหาอ
DD
3
4(1+F)

=

เมื่อ ൌ Ͳ และ F’= 0 ัตราเลือดชิด (F) ได้จากสูตร F = mb ได้จากสูตร F = mb

4
จาก 3+F +4F จาก
′
r DD =
4(1+F)
b = √ 1+F ′ ′ 1+F √ = b
2 2
ท าการแทนค่า m และ b ท าการแทนค่า m และ b
2
F = mb 2 mb = F
2 2
1+F +2F1+F ′ ′′ ′ ′ 1+F 1+F +2F ′′ ′
× (√
= ) × (√ ) =
2(1+F )2 ′ ′ 2 2(1+F )
1+F +2F1+F ′′′ ′ ′ 1+F+2F ′′′ 1+F
= ×× =
2(1+F )2 ′ ′ 2F ) 2(1+